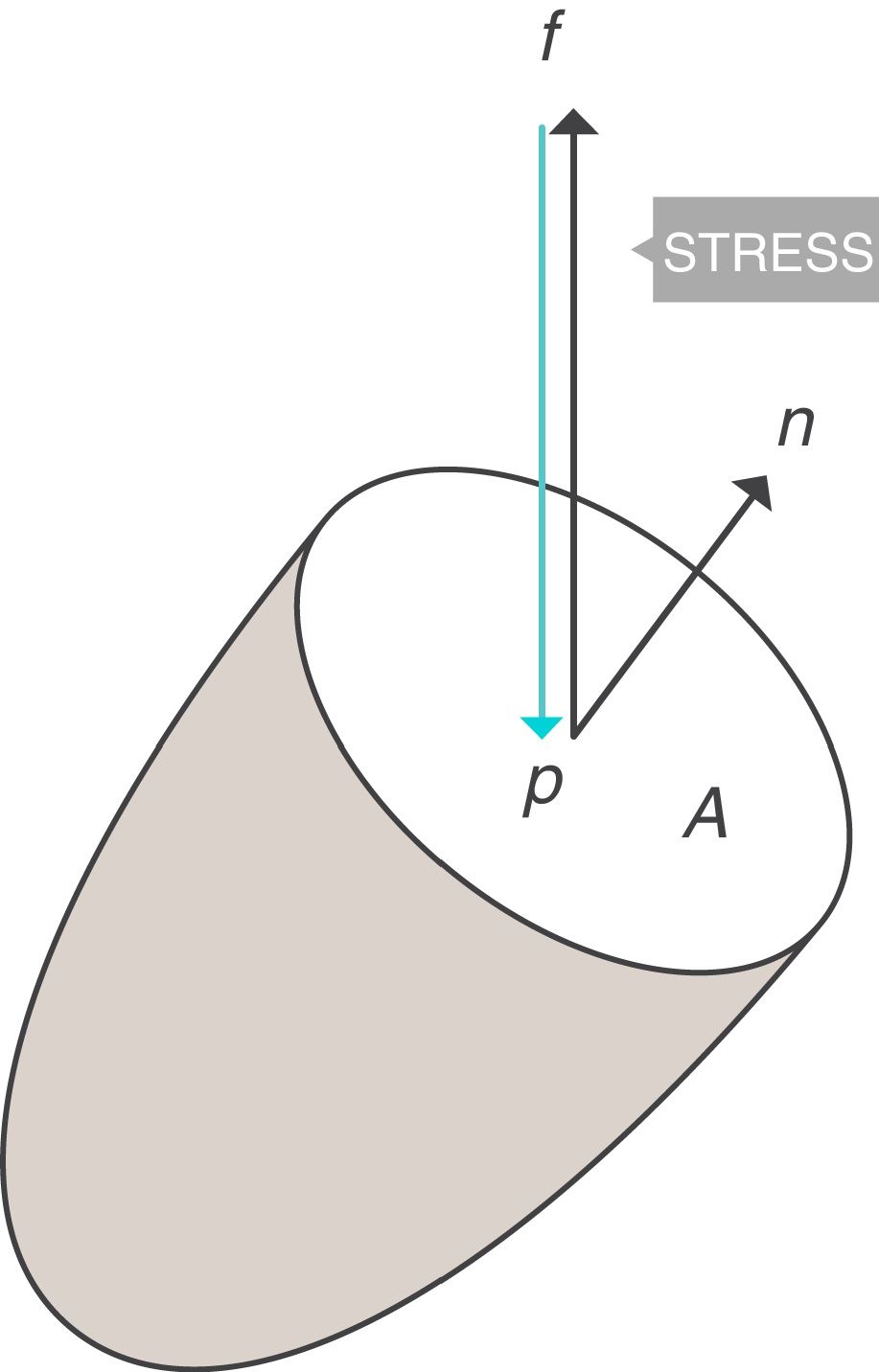
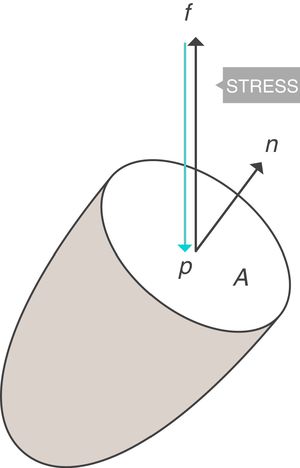
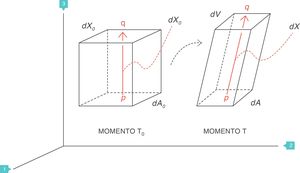
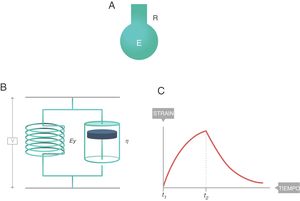
Sea un punto p situado en el interior de un cuerpo, y un plano que corta trasversalmente el cuerpo por el punto p. Sea A el área que corresponde a la superficie de sección del cuerpo por el punto p (fig. 1)3. Si sobre ese cuerpo se aplica una fuerza f, se define stress soportado por el material en el punto p (tensión) a una presión:

Figura 1.

Stress=presión. Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,04MB).

(Ecuación 1)

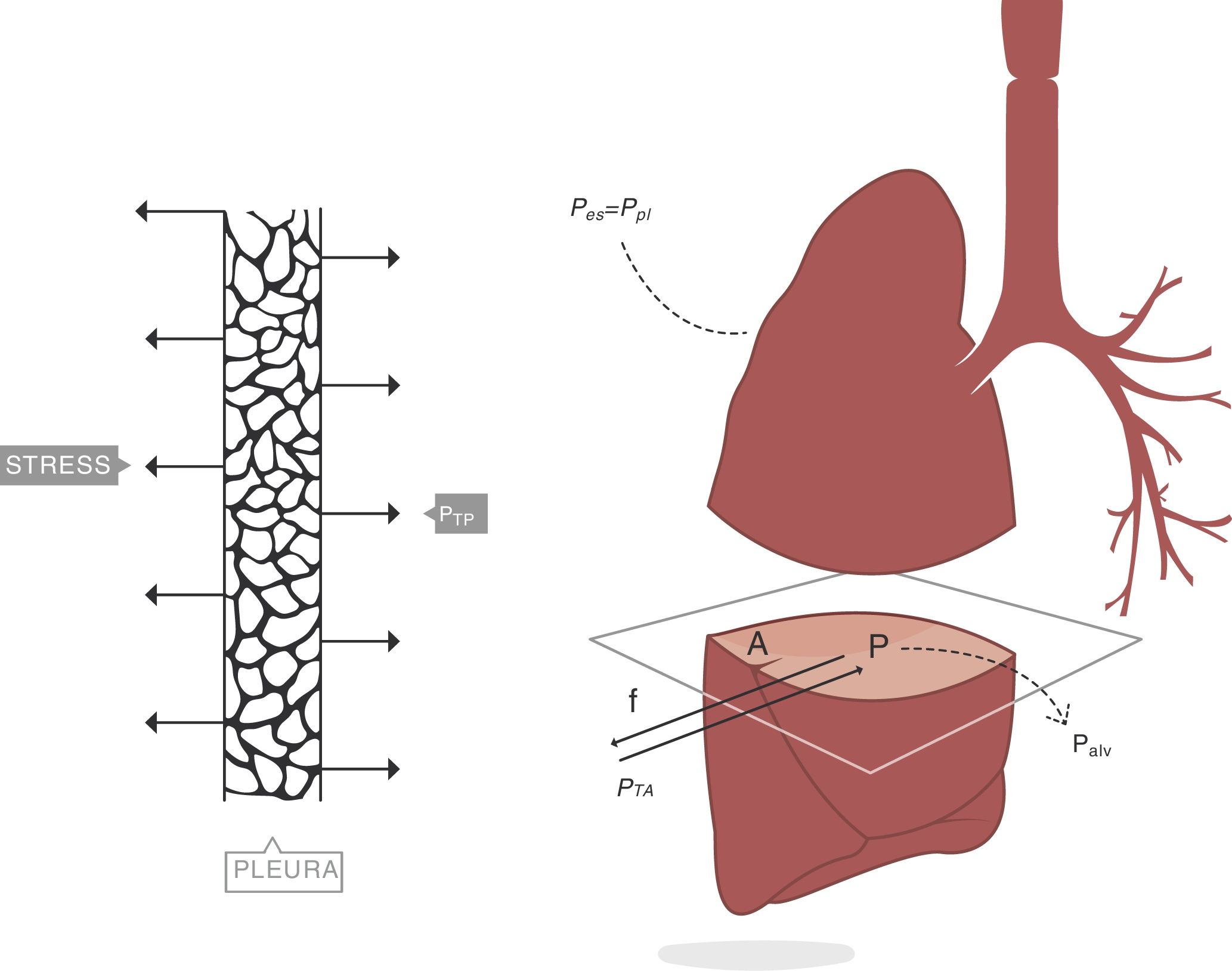
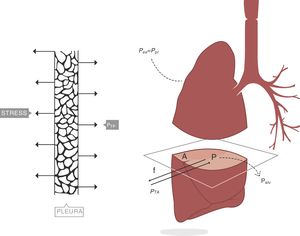
Consideremos ahora el pulmón4. Un plano ideal que lo atraviese deja en su interior una superficie de parénquima limitada por la pleura, cuya área de sección es A. La presión transpulmonar (PTP) es la diferencia entre la presión alveolar (Palv) y la presión en el interior del espacio pleural (Ppl). Se asume que en clínica la presión del espacio pleural (presión mediastínica) puede estimarse midiendo la presión esofágica (Pes). Por tanto (fig. 2):

Figura 2.

Presión transpulmonar (PTP)=presión de retracción. A: superficie A; f: fuerza; P: punto P; Palv: presión alveolar; Pes: presión esofágica; Ppl: presión pleural. Fuente: reproducida con permiso de Modesto-Alapont V et al.26

(0,13MB).

PTP: presión transpulmonar; Palv: presión alveolar; Pes: presión esofágica.

(Ecuación 2)

La PTP es un vector de la misma intensidad (módulo), pero de dirección opuesta a la fuerza que el pulmón hace para retraerse y, por tanto, mide la magnitud de esa fuerza. Por eso también se llama presión de retracción del pulmón.

Es un hecho bien contrastado de la fisiología respiratoria5 que la fuerza que produce que los pulmones se llenen o vacíen de aire y cambien de volumen es el cambio en la PTP (ΔPTP). Por tanto, si aplicamos el concepto reológico de stress a la tensión a la que se somete al tejido pulmonar cuando lo hacemos cambiar de volumen, será:

PTP: presión transpulmonar; Palv: presión alveolar; Pes: presión esofágica.

(Ecuación 3)

Un detalle muy importante que tener en cuenta es que, por definición, la PTP es una medida estática: ha de ser medida en ausencia de flujo mediante las maniobras de pausa inspiratoria y pausa espiratoria de nuestros respiradores.

Desde el punto de vista práctico, el pulmón parte de una posición de reposo (PTP del volumen de reposo telespiratorio) y al final de la inspiración alcanza otra posición de reposo (PTP del volumen teleinspiratorio). Por tanto, durante la inspiración el stress aumenta de magnitud y alcanzará su máximo (= f/A) en la meseta inspiratoria (Pplat). Cuando vuelve el reposo es cuando se igualan stress y ΔPTP. En esos puntos de reposo la fuerza total es igual a 0, ya que en caso contrario el cuerpo se seguiría acelerando (en el caso del pulmón seguiría aumentando de volumen). El proceso contrario se produce en la espiración cuando el pulmón vuelve al estado basal de reposo.

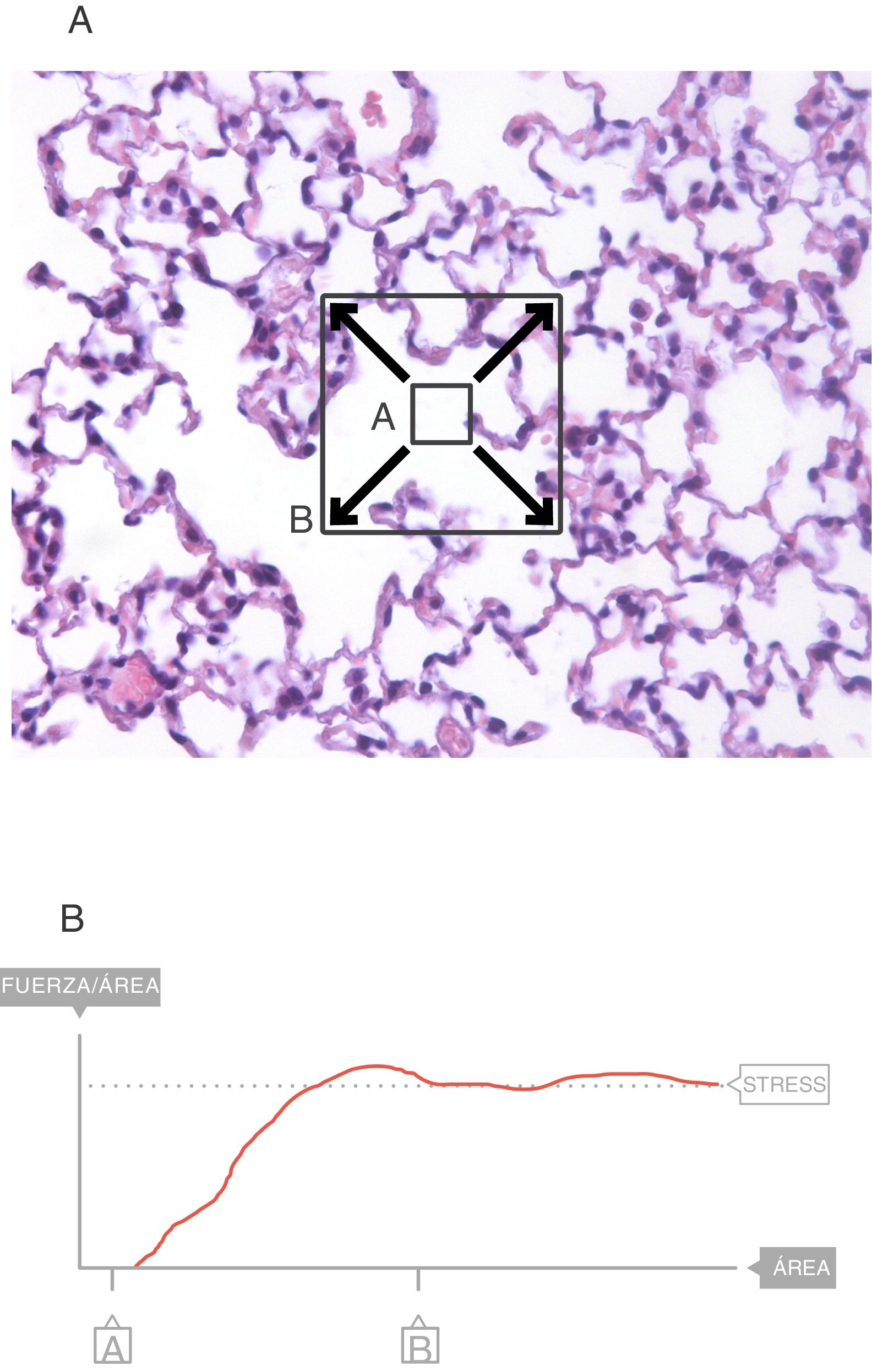
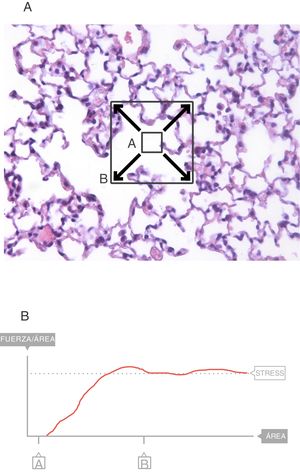
En el interior del parénquima (fig. 3A) las fuerzas son transmitidas a través del plano de corte por los elementos del tejido y la tensión superficial4. Los cuadrados A y B denotan el área que se expande en el seno de la superficie de este corte del tejido. Sobre esa área es sobre la que se mide el stress. El valor del límite máximo (fig. 3B) de la fuerza por unidad de área es el stress6.

Figura 3.

Stress=incremento de presión de retracción (incremento de presión transpulmonar=ΔPTP). Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,29MB).

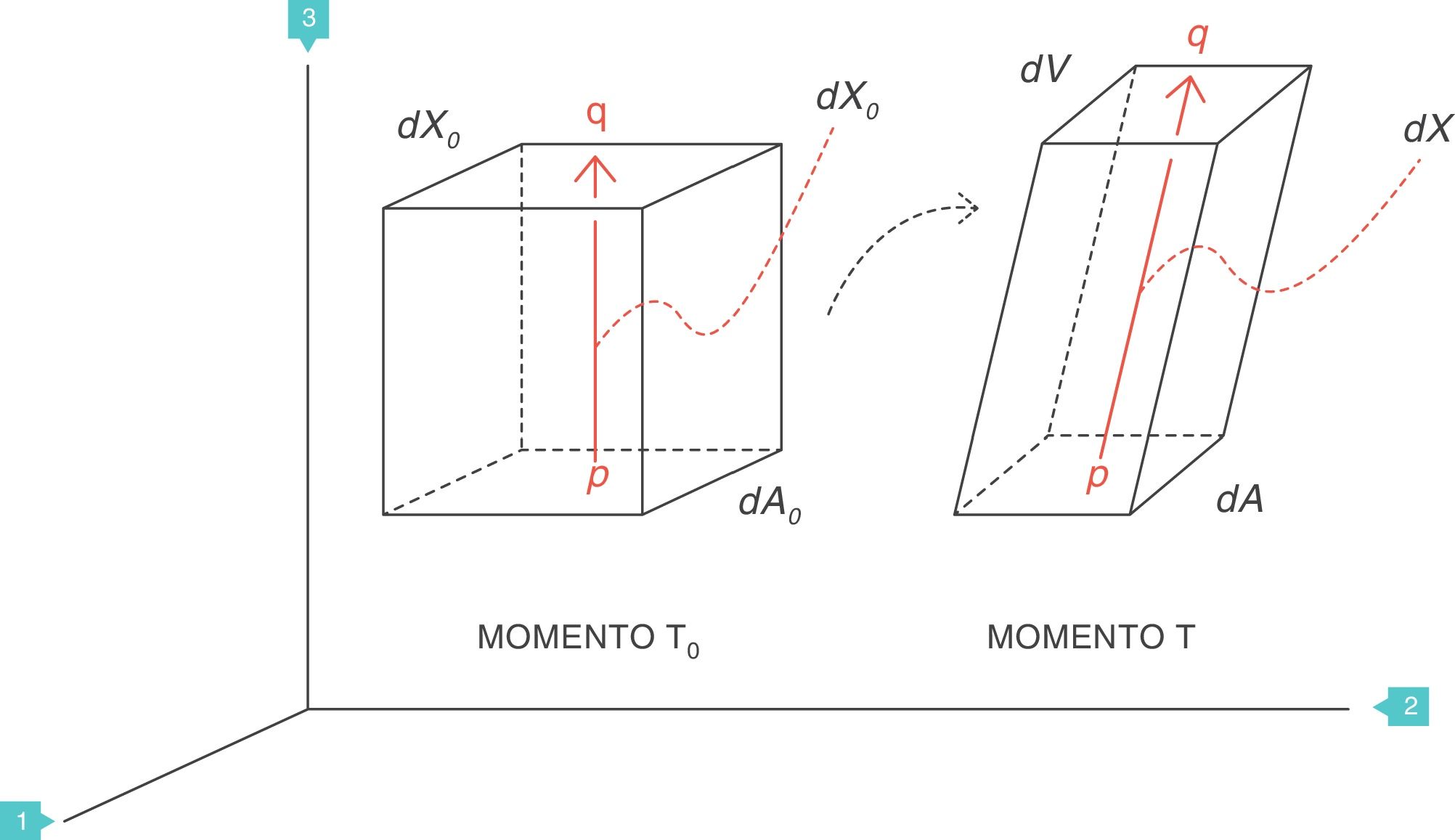
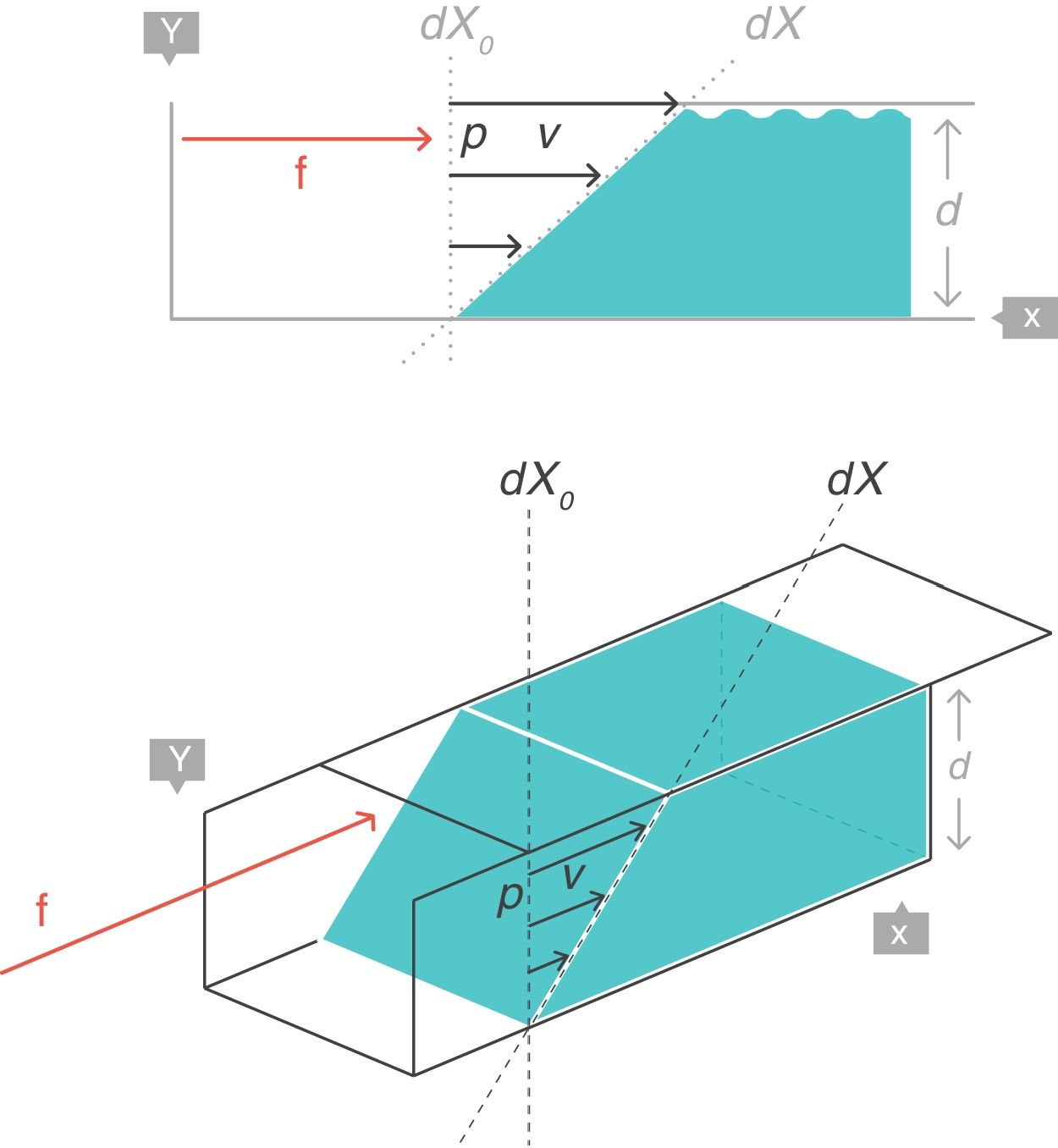
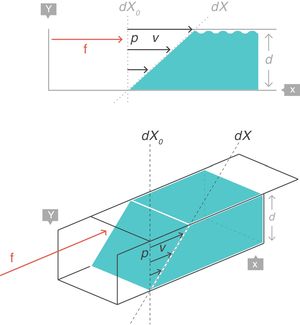
Supongamos que, en el interior de un cuerpo sólido, existen 2puntos p y q separados originalmente una distancia dX0, que puede ser infinitesimal (fig. 4)3. Al aplicar una fuerza f se producirá una deformación en dicho cuerpo sólido, por lo que ambos puntos (p y q) quedarán desplazados de su posición original y separados por nueva distancia dX.

Figura 4.

Strain=deformación (volumen corriente/capacidad residual funcional). Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,08MB).

En reología, la deformación multidimensional que ha sufrido el cuerpo por la acción de la fuerza se caracteriza con el concepto de strain o desplazamiento relativo, que es el cambio que ha sufrido la distancia que separaba los 2puntos p y q (dX − dX0), pero relativo a (dividido por) la distancia original dX0:

(Ecuación 4)

Desde el punto de vista matemático, esta deformación puede ser representada mediante el concepto de derivada. Pero para entender mejor el concepto, se puede recurrir a ejemplos del mundo real con los que estamos familiarizados en la era de los móviles y las computadoras con pantallas táctiles: el strain intenta medir la potencia del «zoom» de una cámara, el cambio en la escala de un mapa o de un objeto visualizados en pantallas táctiles sobre el que apoyamos y desplazamos nuestros dedos índice y pulgar.

La deformación es un fenómeno físico local que aparece en la vecindad de cada uno de los puntos del interior de un sólido. La fuerza que lo deforma hace que este cambie «la escala» de su dimensión: produce el desplazamiento (diferencia en sus distancias de separación) que sufren puntos vecinos en su interior. Por tanto, la deformación de un sólido se producirá solo si ese desplazamiento se define como una función de la distancia original que separaba cada uno de esos puntos vecinos. En términos de análisis matemático, la deformación es la derivada del desplazamiento respecto de la distancia original. El concepto puede generalizarse fácilmente a 2(áreas, dA), 3(volúmenes, dV) o incluso a más dimensiones espaciales.

El strain es adimensional: no tiene unidades. Se representa con un número o, en ingeniería de materiales, como un porcentaje. Su valor es positivo cuando la forma del objeto sólido se engrandece (expansión) y negativo cuando el sólido se contrae. Y su magnitud depende tanto del desplazamiento o gradiente de distancias (numerador) como de la forma original (denominador).

En la fisiología respiratoria clásica, no existe el concepto de strain. Se llama volumen corriente (Vc) a la diferencia entre el volumen de final de inspiración y de la espiración, y en ventilación mecánica corresponde al volumen de aire que ha introducido en los pulmones el respirador. Y se llama capacidad residual funcional (CRF) al volumen de aire que queda rellenando el sistema respiratorio al final de la espiración del Vc. Sin embargo, desde el punto de vista de la reología, en el parénquima pulmonar ocurre como en el resto de los cuerpos sólidos: el tejido se deforma si, por acción de una fuerza, aparece un desplazamiento diferente punto a punto. Por ello, en el sistema respiratorio el strain será igual a:

Vc: volumen corriente; CRF: capacidad residual funcional.

(Ecuación 5)

Supongamos ahora una fina película de un cuerpo líquido. Está contenida entre 2placas metálicas paralelas, separadas una distancia d (fig. 5)3. En su interior existe un punto p separado del origen de coordenadas una distancia dX0, que puede ser infinitesimal. Sobre este punto p se aplica, durante un tiempo dt, una fuerza f. Esta fuerza produce el desplazamiento de la «porción superior» del líquido respecto del resto, con una velocidad constante v que hace recorrer al punto p en el tiempo dt una distancia (dX − dX0) hasta llegar a la nueva posición. Esta nueva posición queda, al final, a una nueva distancia dX del eje de coordenadas.

Figura 5.

Strain rate. Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,07MB).

De nuevo, la manera más apropiada de describir el cambio de configuración (dX − dX0) que ha sufrido el líquido por acción de la fuerza durante el tiempo dt queda representada por el concepto matemático de derivada. En este caso, la velocidad de deformación ostrain rate, que es la velocidad que ha adquirido la «porción superior» del líquido relativa a la posición original (la distancia dX0) que ocupaba en el seno del líquido (que es la de la «porción inferior» que ha permanecido inmóvil). Nótese la equivalencia y las unidades.

t: tiempo.

(Ecuación 6)

Como demuestra esta igualdad algebraica, la velocidad de deformación (strain rate) expresa también las diferentes velocidades de desplazamiento a las que serían sometidos ambos extremos de un objeto líquido cuya longitud inicial fuera d. Es el gradiente espacial en velocidades de desplazamiento. El concepto también puede generalizarse fácilmente de una (longitud, dX) a 2(áreas, dA), 3(volúmenes, dV) o más dimensiones espaciales.

La strain rate tiene unidades de 1/segundos (s−1) y solo tiene valor durante el movimiento: su valor será 0 cuando la velocidad de deformación es 0, es decir, en reposo. Al ser un cociente, su magnitud depende tanto de la velocidad de la deformación (numerador) como de la forma original (denominador).

En la fisiología respiratoria clásica, tampoco existe el concepto correspondiente a strain rate. Se llama flujo aéreo (flujo o caudal) al cociente entre el Vc y el tiempo (t) de inspiración/espiración. Y, por tanto, en términos de la fisiología clásica, se define la strain rate del sistema respiratorio como:

Vc: volumen corriente; CRF: capacidad residual funcional; t: tiempo.

(Ecuación 7)

Para generar conocimiento sobre el comportamiento físico de cada cuerpo, la reología realiza lo que se llaman experimentos tensionales. Somete a los diferentes materiales sólidos a una tensión axial creciente hasta que se produce su fractura o rotura. El comportamiento de cada material se describe mediante lo que se llama la curva tensión-deformación(stress-strain):

• •

  Los materiales sólidos difieren entre sí por la forma específica que adquiere su curva stress-strain.

• •

  La forma de la curva stress-strain de cada uno de los materiales depende a su vez de varios factores: composición química, calentamiento, temperatura, deformidad plástica inicial y velocidad de deformación (strain rate).

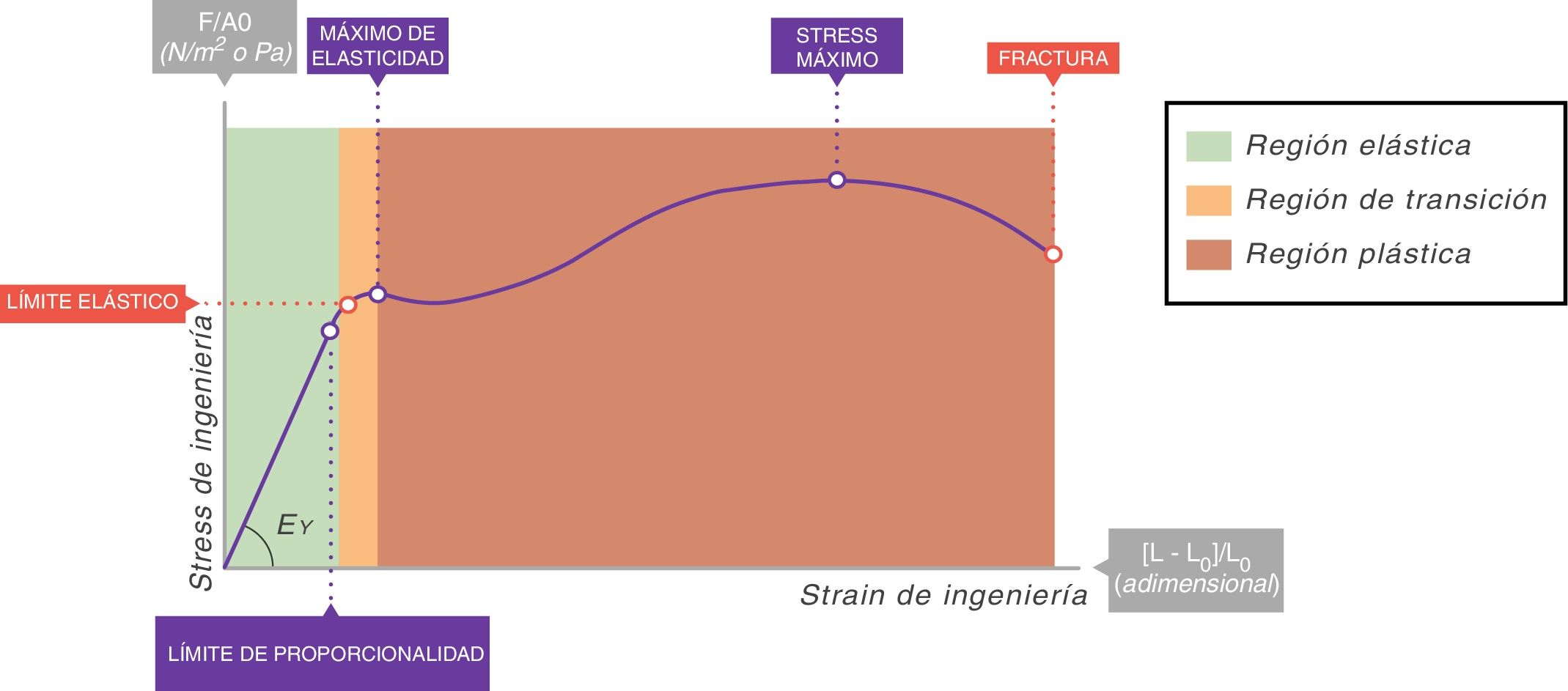
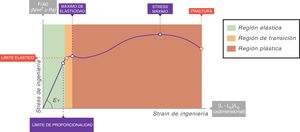
En todas las curvas stress-strain puede identificarse una zona inicial que es lineal y que define su comportamiento elástico (fig. 6)7. A la ecuación de esa parte lineal se le denomina ecuación constitutiva de un sólido elástico (Ley de Hooke):

Figura 6.

Curva stress-strain. EY: módulo de elasticidad de Young. Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,09MB).

EY: módulo de elasticidad de Young

(Ecuación 8)

La constante de proporcionalidad (la pendiente de esta recta) EY (cmH2O) se denomina módulo de elasticidad de Young del sólido. La existencia de un módulo de Young es lo que define al material que estamos estudiando como un sólido: cada sólido tiene un valor diferente de EY.

Un sólido ideal perfecto (al que los físicos llaman cuerpo sólido de Hooke) es completamente elástico: su curva stress-strain es completa y exclusivamente lineal. Se deforma elásticamente y la energía requerida para la deformación se almacena en su interior y se recupera del todo cuando se retira el esfuerzo aplicado. En un sólido que no sea perfecto, si nos mantenemos en esta zona de elasticidad (área verde de la fig. 6), la energía también se recupera por completo sin pérdidas entrópicas significativas.

La mayoría de los metales y cerámicas, ante deformaciones pequeñas, se comportan como cuerpos de Hooke. Pero ningún solido de la naturaleza es un sólido ideal. En la curva stress-strain de todos ellos, más allá de la zona de proporcionalidad (límite elástico), empieza una zona de comportamiento plástico (área roja, fig. 6), en la que la deformación induce deformidad. Parte de la energía no se recupera totalmente cuando cesa la tensión y se disipa en el interior del sólido produciendo cambios estructurales permanentes en la forma original. Por tanto, comienzan a aparecer «lesiones» o microfracturas (fatiga del material) que deforman plásticamente la estructura.

Más allá de esta zona plástica, si la tensión sigue aumentando, se produce la rotura/fractura del material.

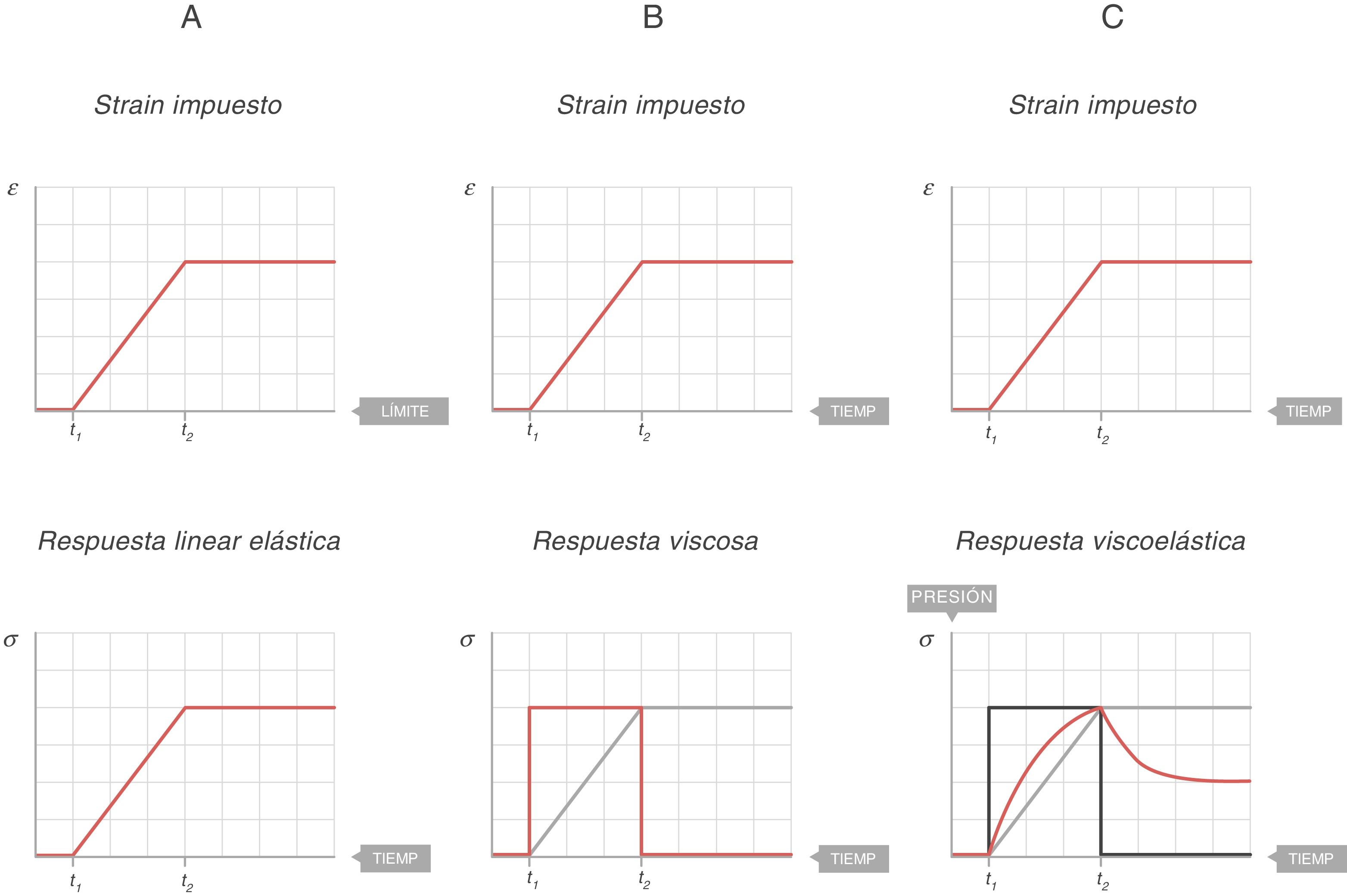
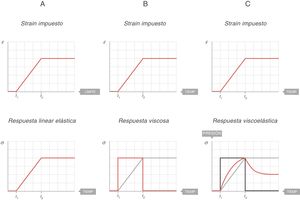
En la figura 7A se representa el comportamiento de un sólido ideal. Si durante un tiempo (t2 − t1) se aplica una fuerza que produce un strain (arriba), el stress soportado por ese cuerpo (abajo) es directamente proporcional al strain producido. Si el strain no desaparece, el stress no disminuye. En un sólido ideal, strain y stress son 2caras de la misma moneda.

Figura 7.

Comportamiento elástico, viscoso y viscoelástico. Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,21MB).

En el caso de los cuerpos líquidos, la reología estudia cómo fluyen estos cuerpos en respuesta a las fuerzas que se les aplican. Para ello describe su rendimiento mecánico en función de las relaciones matemáticas entre el stress soportado por el líquido cuando se le aplica una fuerza y el strain rate, la velocidad con la que se produce la deformación (la derivada del strain con respecto al tiempo).

Un líquido ideal perfecto (al que los físicos llaman fluido de Newton) se comporta de acuerdo con la ecuación constitutiva de un líquido:

η: módulo de viscosidad.

(Ecuación 9)

Se llama módulo de viscosidad del líquido a la constante η (cmH2O×segundos). La existencia de un módulo de viscosidad es lo que define al material que estamos estudiando como un líquido: cada líquido tiene un valor diferente de η.

Los fluidos se comportan de manera completamente diferente a los sólidos. Cuando se aplica una fuerza a un líquido ideal, el stress soportado por el líquido hace que este se deforme de manera irreversible, que «fluya». La energía requerida para la deformación se disipa completamente por el interior del fluido en forma de calor y de entropía y no se puede recuperar cuando cede la fuerza y se retira el esfuerzo.

En la figura 7B se representa el comportamiento de un líquido ideal. Si durante un tiempo (t2 − t1) se aplica una fuerza que produce una deformación (arriba), el stress soportado por ese cuerpo (abajo) se comporta de manera diferente a lo que ocurría en un sólido. Ahora no es directamente proporcional al strain producido, sino que es directamente proporcional al strain rate; es decir, a la velocidad con la que se ha producido esa deformación. En el líquido, la forma de la función con la que se ha ganado el strain es una recta, la velocidad de ese strain es la derivada de esa recta: una constante durante todo el tiempo que dura el movimiento. Por tanto:

• •

  Solo durante el tiempo que ha habido movimiento el líquido ha sufrido stress, en este caso un stress constante.

• •

  Cuando el movimiento cesa, el stress se hace 0.

• •

  La energía requerida para la deformación se ha gastado en calentar y hacer fluir el líquido.

La mayoría de los materiales de la naturaleza muestran un comportamiento reológico intermedio entre los líquidos y los sólidos. Son a la vez elásticos y viscosos y, por ello, desde el punto de vista físico se les denomina cuerpos viscoelásticos.

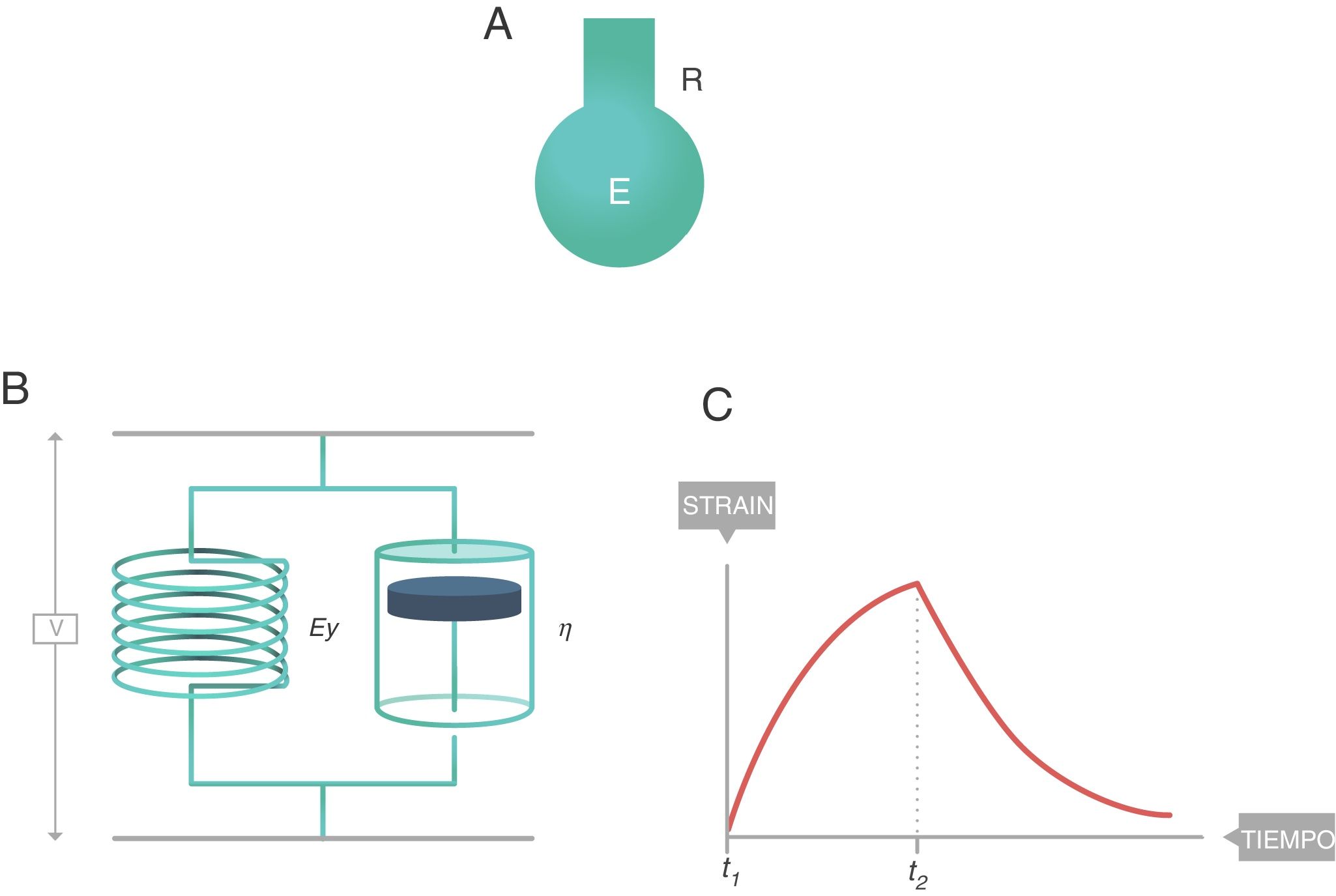
En reología, el comportamiento de los cuerpos viscoelásticos se modeliza de diferentes maneras: cuerpo de Maxwell, cuerpo de Kelvin, etc. El modelo que parece explicar con mayor exactitud el comportamiento biofísico del sistema respiratorio es el de 8 parámetros de Bates8, cuya descripción detallada excede el ámbito de este artículo. Sin embargo, el modelo simple (monocompartimental) que lo explica con la suficiente exactitud como para poder ser utilizado en clínica es el cuerpo sólido de Voigt. Está formado por un muelle (módulo de elasticidad, EY) y un amortiguador (módulo de viscosidad, η) conectados en paralelo. Este modelo se caracteriza porque:

• •

  El stress global soportado por el sólido de Voigt completo es la suma de los stress soportados por cada uno de sus componentes.

• •

  El strain inducido en cada uno de los elementos es el mismo e igual al strain inducido en todo el sólido de Voigt.

La ecuación constitutiva de los cuerpos viscoeláticos aplicable al sólido de Voigt se denomina ecuación de Voigt (fig. 8):

Figura 8.

Cuerpo viscoelástico de Voigt. E: elastancia; EY: módulo de elasticidad de Young; R: resistencia; η: módulo de viscosidad. Fuente: reproducida con permiso de Modesto-Alapont V, et al.5.

(0,07MB).

EY: módulo de elasticidad de Young; η: módulo de viscosidad.

(Ecuación 10)

De esta ecuación se puede deducir otra que rige temporalmente la deformación en un cuerpo de Voigt cuando es sometido a un stress constante durante un tiempo (t2 − t1):

t: tiempo; τ: constante de tiempo.

(Ecuación 11)

Esta ecuación es una función de la constante τ (segundos), la llamada constante de tiempo del cuerpo de Voigt, cuyo valor es:

τ: constante de tiempo; η: módulo de viscosidad; EY: módulo de Young.

(Ecuación 12)

En la figura 7C se representa el comportamiento de un cuerpo viscoelástico9. Es un comportamiento intermedio entre el sólido y el líquido ideales:

• •

  Si durante un tiempo (t2 − t1) se aplica una fuerza que produce una deformación (arriba), durante el tiempo que hay movimiento el cuerpo soporta un stress (línea azul) intermedio entre el que soportaría si fuera un sólido (proporcional al strain) y si fuese un líquido (proporcional al strain rate).

• •

  Cuando el movimiento cesa, el stress producido por el strain rate desaparece. Esa energía ha sido utilizada en calentar el cuerpo y se ha disipado por su interior.

• •

  Pero queda el stress producido por el strain y, por ello, el stress total cuando cesa el movimiento queda a un nivel intermedio entre el que soportaría si fuera un sólido y el que tendría si fuera un líquido (que sería 0).

Este fenómeno está modelizado también en el cuerpo de Voigt. Una vez superado el tiempo (t2 − t1) en el que se le aplica la fuerza, cuando el cuerpo de Voigt se deja libre (stress relaxation) este sistema viscoelástico revierte la deformación con una pérdida del strain que sigue la ecuación:

t: tiempo; τ: constante de tiempo.

(Ecuación 13)

Es fácil reconocer, en el perfil de la figura 7C, el trazado de la fase inspiratoria de la curva presión-tiempo en modo controlado por volumen con flujo cuadrado. Así que, desde el punto de vista físico, es razonable suponer que el sistema respiratorio se comporta como un cuerpo viscoelástico. De hecho, en ventilación mecánica se han descrito al menos 3fenómenos que se asocian al comportamiento viscoelástico del sistema respiratorio:

• 1.

  La histéresis dinámica (en el bucle dinámico P-V)10.

• 2.

  La stress relaxation (diferencia P1 − P2 tras una pausa inspiratoria de 5 s)11.

• 3.

  El índice de stress12.

La fisiología clásicamente propuesta para explicar el funcionamiento del sistema respiratorio13, que hasta ahora estamos utilizando para entender la ventilación mecánica, asume que durante una respiración normal la energía se utiliza para vencer 2fuerzas: la presión resistiva y la presión elástica. Con ello se asume que el comportamento del sistema respiratorio se rige por la ecuación de movimiento:

P: presión; t: tiempo; E: elastancia; R: resistencia.

(Ecuación 14)

donde, para cada instante particular t, P(t) es la presión aplicada por el respirador, V(t) es el volumen corriente entregado, F(t) es el flujo al que se entrega ese volumen, que corresponde a la derivada del volumen con respecto al tiempo [F(t)=dV(t)/dt], y presión positiva al final de la espiración (PEEP) es la presión que existe en la vía aérea al final de la espiración14.

Esta ecuación está en función de 2constantes: R, la resistencia de la vía aérea al flujo del aire y E, la elastancia del parénquima pulmonar (o su inversa, la complianza, C=1/E).

El producto de la complianza y la resistencia es otra constante, la constante de tiempo (τ=C×R=R/E), que resume el comportamiento global del sistema respiratorio desde el punto de vista físico. La presión resistiva es la presión utilizada para vencer la resistencia y se hace 0 cuando el flujo desaparece.

La fisiología clásica ha asumido que el sistema respiratorio, cuya ecuación constitutiva es esta ecuación de movimiento, podría teóricamente modelizarse como un modelo simple monocompartimental: «cuerpo elástico-resistivo»15. Se trata de un cuerpo teórico semejante al cuerpo de Voigt, pero en el que el coeficiente de elasticidad de Young EY del muelle queda representado por la elastancia (E) del parénquima pulmonar y el coeficiente de viscosidad (η) del amortiguador queda representado por la resistencia (R) de la vía aérea. Cuando el modelo gana volumen a flujo constante tiene un comportamiento que recuerda al de un cuerpo viscoelástico de la reología. Parte de la energía aplicada se disipa en el interior del elemento resistivo (R) y la otra parte se acumula en el elemento elástico (E), constituyendo la presión de conducción de la espiración.

Sin embargo, si se analiza con detenimiento la ecuación de movimiento del sistema respiratorio, se puede apreciar que no es idéntica a la ecuación de Voigt. Además de añadirse la PEEP:

• •

  Se sustituye EY por E.

• •

  Se sustituye η por R.

• •

  Se sustituye el strain por el volumen corriente entregado V(t).

• •

  Se sustituye el strain rate por el flujo F(t).

Y, como hemos visto, para la reología no es lo mismo strain que volumen corriente, ni flujo que strain rate. Estas diferencias son capitales, tanto desde el punto de vista teórico como práctico. Así que ¿es razonable esta aproximación clásica o existen datos experimentales de que el sistema respiratorio humano es físicamente un cuerpo viscoelástico como el que estudia la ciencia de materiales? Si este fuera el caso, ¿deberíamos empezar a aplicar los conceptos reales de la reología, o nos conformamos con su sucedáneo elástico-resistivo? ¿Es posible que la reología «genuina» explique mejor el fenómeno de la producción del VILI?

En 2011 Gattinoni realizó un experimento con diseño caso-control16 en cerdos sanos ventilados artificialmente. La variable de resultado era la presencia necrópsica de VILI tras 60 h de ventilación, y describió la existencia de un módulo de Young (EY) en el sistema respiratorio: una relación de proporcionalidad lineal entre el strain y el stress. Es decir, demostró que el sistema respiratorio es reológicamente un sólido elástico, porque se cumple la ecuación constitutiva de un sólido (ley de Hooke).

Utilizando las definiciones reológicas de strain y stress y el concepto clásico de elastancia pulmonar:

E: elastancia; C: complianza: PTP: presión transpulmonar; Vc: volumen corriente.

(Ecuación 15)

Puede calcularse que:

EY: módulo de Young; PTP: presión transpulmonar; Vc: volumen corriente; CRF: capacidad residual funcional.

(Ecuación 16)

Por tanto:

EY: módulo de Young; E: elastancia; C: complianza; CRF: capacidad residual funcional.

(Ecuación 17)

De estas ecuaciones podemos concluir que no existe equivalencia directa entre EY y E y, por tanto, entre el modelo reológico y el clásico elástico-resistivo. Esta inconmensurabilidad entre ambos paradigmas comporta, a priori, un grave problema para la aplicación directa del modelo reológico en la clínica diaria, ya que el valor de la CRF (necesario para medir el strain) y el stress pulmonar son difíciles de medir a la cabecera de un enfermo crítico. La razón fundamental es que no hay correlación17 entre CRF y PEEP ni entre ΔPTP y Vc, los parámetros de la ventilación mecánica teóricamente candidatos a ser sus mejores representantes.

A ese módulo de Young (EY) del sistema respiratorio, se le denomina elastancia pulmonar específica (ESL).

EY: módulo de Young; PTP: presión transpulmonar; ESL: elastancia específica del pulmón; Vc: volumen corriente; CRF: capacidad residual funcional.

(Ecuación 18)

Como puede deducirse de esta ecuación, su valor coincide con el gradiente de PTP, que produce que la cantidad de aire que rellena el interior de los pulmones sea el doble del valor de la CRF (es decir, produzca la entrada de un Vc que iguale en magnitud a la CRF, con lo que el strain sería igual a 1). En el cerdo sano, la elastancia pulmonar específica vale 5,4±2,2 cmH2O. A su inversa, se le denomina complianza pulmonar específica (CSL), y tampoco equivale directamente a la C del modelo clásico:

ESL: elastancia específica del pulmón; CRF: capacidad residual funcional; C: complianza; CSL: complianza específica del pulmón.

(Ecuación 19)

El equipo de Gattinoni descubrió además que la proporcionalidad directa entre stress y strain se conserva intacta para valores de strain inferiores a 1, pero la relación comienza a perder su linealidad para valores de strain entre 1,5 y 2. La reología predice, pues, que a partir de ese límite elástico comienza el VILI: la deformación pulmonar ya no es totalmente reversible y empiezan a producirse microfracturas y roturas (deformidades establecidas). Y esa predicción ha sido validada en este mismo experimento y, como veremos luego, en otros posteriores. En este, la probabilidad de presentar VILI crecía logísticamente con el valor del strain: el valor del strain era de 1,29±0,57 cuando no existía VILI, y de 2,16±0,58 (p <0,001) cuando lo había. Y más importante aún, todos los cerdos sin VILI sobrevivían al experimento, pero la mortalidad de los cerdos con VILI tras solo 60 h de ventilación era del 86%.

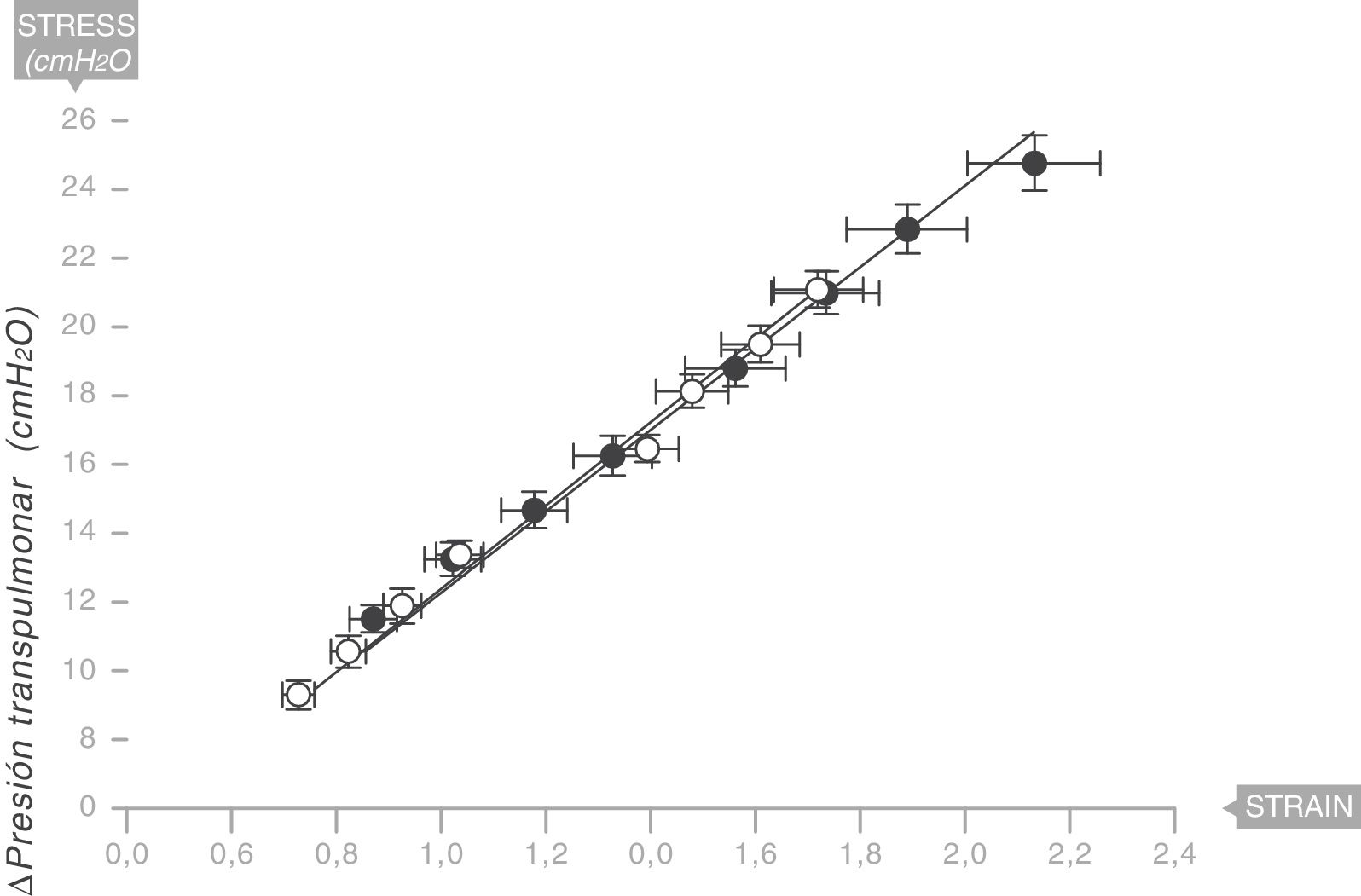
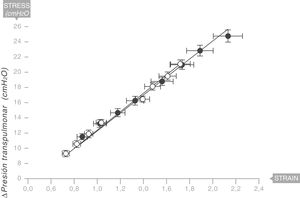
En 2008, aunque esta vez sin confirmación anatomopatológica, el mismo equipo liderado por Gattinoni y Marini18 describieron la existencia de un módulo de Young en los pulmones de una serie de pacientes ventilados por síndrome de distrés respiratorio agudo (SDRA) (fig. 9). Por tanto, el pulmón humano es también reológicamente un sólido elástico. El valor de la elastancia específica en el pulmón del adulto humano con SDRA es ESL=13,5±4,1 cmH2O (intervalo de confianza [IC] al 95%: 11,8 a 15,2). Este valor es constante independientemente de la causa del SDRA y del Vc o la PEEP usados en la ventilación.

Figura 9.

Módulo de Young en el pulmón de pacientes con síndrome de distrés respiratorio agudo (SDRA) (círculos sólidos) y pacientes control (círculos blancos). La elastancia específica del pulmón es igual a 13,5±4,1 cmH2O. Fuente: modificado y reproducido con permiso de Chiumello et al.18.

(0,05MB).

En niños con SDRA, el mismo equipo de investigadores ha encontrado que el valor de la elastancia específica en el pulmón pediátrico es ESL=13,5 (IC 95%=10 a 15,3) cmH2O. Dicho valor no se modifica con la edad19.

En 2012, confirmando lo que predice la reología y reproduciendo en pacientes adultos con SDRA tipo ALI lo que había descrito Gattinoni en su modelo experimental, los investigadores españoles liderados por Albaiceta et al.20. encontraron una correlación directa entre la magnitud del strain inducido por la VM y los valores de IL-6 e IL-8 en el lavado broncoalveolar. Para medir la CRF, en este trabajo se utilizó un método de lavado (washin/washout) de oxígeno, y en todos los pacientes se utilizaron Vc en torno a 7mL/kg. Sin embargo, en los pacientes con mayor inflamación pulmonar se utilizaron PEEP menores (se objetivó menos aire en su CRF al final de la espiración) y presiones de conducción de 22,6±6 cmH2O.

Ya hemos visto antes que el modelo reológico y el elástico-resistivo clásico parecen 2paradigmas inconmensurables. La principal dificultad para encontrar la equivalencia entre ambos, y poder utilizar el modelo reológico en la clínica diaria, es la dificultad para estimar el valor de la CRF a pie de cama, con un respirador artificial convencional.

Sin embargo, se han dado varios pasos importantes. Marini et al. han estudiado21 la relación entre el stress del modelo reológico (ΔPTP, cmH2O]) y la driving pressure o presión de conducción (DP, cmH2O), que es la diferencia entre la presión meseta Pplat (pausa inspiratoria) y la PEEP total (pausa espiratoria), parámetros ambos fáciles de estimar. Y en relación con el valor del cociente ΔPTP/DP, se ha establecido que:

• •

  Oscila entre 0,46 y 0,79 en diferentes situaciones clínicas, incluidos los pulmones sanos.

• •

  El valor en los pulmones con SDRA es 0,75.

• •

  Esta relación disminuye cuando aumenta el valor de la presión intraabdominal, excepto en situaciones de SDRA.

• •

  El valor de la PEEP no afecta a la relación ΔPTP/DP.

Chiumello et al.17 han replicado de manera independiente estos hallazgos y han encontrado también una correlación muy estrecha (R2=0,7; p <0,001) entre el stress y la DP. En pulmones con SDRA el stress corresponde al 73-85% de la DP: ΔPTP/DP=0,73 a 0,85.

Por tanto, considerando que:

• 1)

  El módulo de Young (elastancia específica) del pulmón humano con SDRA es aproximadamente de 13 cmH2O.

• 2)

  Una VM que produzca en el pulmón un strain mayor o igual a 1 será la que empiece a producir una VILI clínicamente relevante.

Puede deducirse que deberíamos considerar clínicamente que debe realizarse la VM sometiendo al pulmón a un stress (ΔPTP) inferior a 13 cmH2O. En su trabajo, Chiumello et al.17 demostraron que la DP puede ser utilizada para determinar si el pulmón está siendo sometido a un grado de stress lesivo. Así, un valor umbral de DP de 15 cmH2O tiene una exactitud diagnóstica muy buena (área de bajo la curva [AUC]=0,864 [IC 95%=0,8 a 0,93]; sensibilidad=0,9; especificidad=0,78; peso de evidencia a favor=7 decibanes; peso de evidencia en contra=−8 decibanes) para detectar que se está sometiendo al pulmón a un stress ≥ 12 cmH2O y, por tanto, se está generando VILI.

En conclusión, parece que la DP es el parámetro básico que conecta la teoría fisiopatológica clásica con el modelo reológico y consigue la equivalencia de ambos paradigmas. Un valor umbral de DP=15 cmH2O, que en humanos corresponde con un strain en torno a 1, parece marcar el nivel de stress tolerable en el límite elástico a partir del cual se induce VILI.

En este mismo sentido, usando la teoría reológica, Rahaman22 ofrece una explicación convincente a un fenómeno establecido con claridad en la clínica: la ventilación mecánica de los pulmones sanos con los parámetros habitualmente utilizados no produce VILI relevante desde el punto de vista clínico. En un pulmón humano sano la CRF son 35mL/kg y la CPT son 85mL/kg23. Si se utiliza una estrategia ventilatoria en la que el volumen teleinspiratorio fuera la CPT y el volumen telespiratorio fuera la CRF, el stress sería:

Esta cifra de stress (ΔPTP) coincide con una presión de conducción (DP) de:

Este valor es claramente superior al valor umbral de DP=15 cmH2O, por lo que con tal estrategia (que induce un strain de 1,5) se está generando VILI en un pulmón sano.

Es fácil deducir que, en este mismo pulmón sano, usar un Vc de 6mL/kg (strain=0,17; stress=2,31 cmH2O; DP=2,89 cmH2O) o incluso un Vc de 10mL/kg (strain=0,29; stress=3,86 cmH2O; DP=4,82 cmH2O) es seguro y no produce VILI. Hay que recordar que esta ha sido la forma tradicional de ventilar los pulmones sanos en la clínica diaria.

La principal evidencia científica ha sido proporcionada por Amato et al.24. Se trata de un metaanálisis de ensayos clínicos publicado en 2015 en NEJM, realizado con los datos individuales de 3.562 pacientes ventilados por SDRA y en el que se utilizan técnicas estadísticas complejas (análisis de mediación multinivel) para minimizar el sesgo de confusión inducido por factores pronósticos conocidos previos a la ventilación mecánica (p. ej. el cociente presión arterial de oxígeno/fracción inspirada de oxígeno [P/F] al entrar al ensayo). De todos los parámetros del ventilador, la DP del primer día de VM fue el más sólidamente asociado con la superviviencia. Por cada incremento en 7 cmH2O en la DP, el riesgo relativo de muerte aumentaba 1,41 (IC 95%: 1,31-1,51; p <0,001). Este efecto se evidenciaba incluso en los pacientes en los que se estaba aplicando ventilación de «protección pulmonar», aunque de forma menos marcada (riesgo relativo [RR]=1,36; IC 95%: 1,17-1,58; p <0,001). Los cambios en el Vc, la Pplat o la PEEP no afectaban a la supervivencia a no ser que con ellos se produjera un cambio en la DP.

Y, además, es importante recordar que en los datos de la enorme cohorte multicéntrica LUNG SAFE25, el parámetro más consistentemente asociado con la mortalidad es la utilización de una DP ≥ 14 cmH2O. Su efecto se muestra en todos los estratos de gravedad del SDRA.