INTRODUCCIÓN

La preocupación por establecer una predicción pronóstica de supervivencia en los enfermos atendidos en los Servicios de Medicina Intensiva es una constante de la investigación clínica en este campo de la asistencia.

A esta inquietud responde el diseño de EPEC (estimación pronóstica en enfermos críticos)1,2, descrito en 2002 por un grupo de clínicos cubanos, y cuya finalidad es proporcionar un nuevo instrumento predictivo caracterizado por su sencillez de aplicación y por estar pensado para prescindir de elementos informáticos o de computación matemática que realicen los complejos cálculos que exige una estimación pronóstica. La descripción del formulario de cómputo de probabilidad pronóstica mediante EPEC se presenta en el anexo 1.

De las condiciones teóricas que exige la construcción de un índice pronóstico de supervivencia: sencillez, reproducibilidad y validación en una muestra distinta de la utilizada para su diseño3,4, la única que EPEC no cumple en su descripción inicial1 es la de validación en una muestra independiente.

El objetivo de nuestro trabajo tiene tres vertientes: utilizar el sistema EPEC en su aplicación a una cohorte de enfermos críticos, validar su diseño en una muestra independiente y comparar la exactitud de las predicciones obtenidas con la de dos sistemas de estimación pronóstica, ampliamente introducidos en la práctica habitual de las Unidades de Cuidados Intensivos (UCI), y de prestaciones bien conocidas, MPM II 0 y SAPS II; todo ello revisando, al mismo tiempo, la metodología de validación del diseño de un sistema pronóstico de supervivencia.

PACIENTES Y MÉTODOS

En un Servicio de Medicina Intensiva, de un Hospital docente de referencia con 19 camas (15 de UCI propiamente dichas y 4 de Cuidados Intermedios), y durante un período de 6 meses del año 2003, se ha recogido de forma prospectiva información suficiente para cumplimentar un CMBD (conjunto mínimo básico de datos) de diseño propio.

El CMBD incluía datos demográficos y epidemiológicos (género, edad, motivo de ingreso, procedencia y tipo de paciente), de funcionamiento del Servicio (estancia, gravedad [sistema SAPS II] y carga de trabajo de enfermería [sistema NEMS, con puntuaciones durante el primer día de estancia y del total de todos los días de estancia]), de resultado asistencial (mortalidad hospitalaria) y de estimación pronóstica de la misma (MPM II 0, SAPS II y EPEC).

La capacidad de discriminación pronóstica por los tres sistemas utilizados (MPM II 0, SAPS II y EPEC) fue establecida mediante el cálculo del área bajo la curva ROC (receiver operating characteristics).

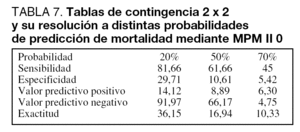
La calibración fue establecida mediante el test C de Hosmer Lemeshow y la exactitud de predicción fue calculada mediante resolución de tablas de contingencia de Stuart Kendall, del tipo 2 x 2, calculadas para puntos de corte de predicción del 20%, 50% y 70%, y de las predicciones medias de mortalidad para MPM II 0, SAPS II y EPEC. La resolución de estas tablas permitió el cálculo de la especificidad (E), sensibilidad (S), valor predictivo positivo (VP+), valor predictivo negativo (VP-) y exactitud de predicción.

La concordancia de las predicciones realizadas por cada uno de los sistemas se estudió mediante el método de análisis de concordancia de Bland Altman, con cálculo de los márgenes de oscilación de los límites del IC 95% (intervalo de confianza del 95% de la diferencia media de probabilidad de predicción para cada paciente) y del número de puntos situados fuera del IC 95%, admitiéndose un 5%, por definición, como cifra tolerable.

En todos los casos los niveles de significación se establecieron si p < 0,05. La abreviatura NS (no significativo) se utilizó cuando p > 0,05.

El estudio estadístico se realizó mediante el programa SPSS/PC 11.0.

RESULTADOS

Se han incluido en el estudio 484 pacientes consecutivos no seleccionados, de los cuales fallecieron (mortalidad hospitalaria) 60 pacientes (12,4%).

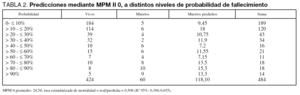
Las tablas 1, 2 y 3 muestran la cifra absoluta de pacientes fallecidos respecto de los predichos muertos para cada intervalo de probabilidad. Las diferencias en el número de pacientes incluidos en cada una de las tablas se justifica por el hecho de no disponer de los datos necesarios para establecer el pronóstico de mortalidad. Las tablas proporcionan, igualmente, los valores de la ratio de la estandarizada (SMR) y su IC 95%.

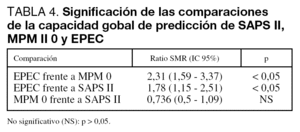
Los análisis de significación de las comparaciones entre la SMR de EPEC y de MPM II 0 y de SAPS II se muestran en la tabla 4, que permite comprobar cómo no existen diferencias significativas entre la SMR de los dos índices más consolidados y sí la hay entre la capacidad de predicción de cualquiera de ellos y EPEC.

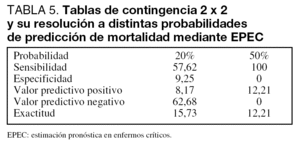
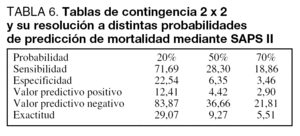
La resolución de las tablas de contingencia elaboradas sobre probabilidades de muerte del 20%, 50% y 70% se presenta en las tablas 5, 6 y 7. Debe destacarse que ninguno de los pacientes evaluados mediante EPEC presentó una probabilidad de muerte mayor del 50%, por lo que en este caso la tabla correspondiente muestra únicamente los datos de resolución alrededor de probabilidades del 20% y 50%.

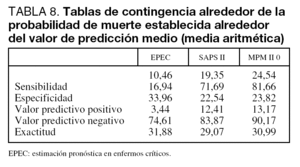
La tabla 8 ofrece los resultados de la resolución de las tablas de contingencia alrededor tanto de la probabilidad de muerte establecida como del valor de predicción medio (media aritmética).

Las ecuaciones de regresión lineal, que permiten la interutilización de los distintos métodos de estimación pronóstica de supervivencia, tienen unos excelentes coeficientes de correlación (R) con una significación de p < 0,05. Los valores son: a) EPEC- SAPS II: R 0,658; p < 0,001; b) EPEC-MPM 0: R 0,704; p < 0,001 y c) SAPS II-MPM 0: R 0,732; p < 0,001.

La calibración de los tres métodos (con las limitaciones a que obliga la restricción de los intervalos de probabilidad a menos de 50% para EPEC), mediante el test C de Hosmer-Lemeshow, puede calcularse a partir de las tablas 1, 2 y 3. Proporciona los siguientes valores: para EPEC, Chi cuadrado 9,66, p < 0,05; para MPM 0, Chi cuadrado 23,76; p < 0,001, y para SAPS 2 Chi cuadrado 12,43; p = NS, resultando pues que para este tamaño muestral sólo SAPS II está bien calibrado en su capacidad de predicción de mortalidad.

La capacidad discriminante de supervivencia se ha estudiado mediante el cálculo de las áreas bajo las curvas ROC (figs. 1 A, B y C) y proporciona los siguientes resultados: 0,836 (IC 95%: IC 0,781-0,891; p < 0,001) para EPEC, 0,839 (0,780-0,899; p < 0,001) para MPM II 0 y 0,827 (0,777-0,876; p < 0,001) para SAPS II.

Figura 1. Capacidad de discriminaciónde los tres métodos. Presentación mediante curvas ROC.A) curva ROC para estimación pronóstica de enfermos críticos (EPEC); B) curva ROC para MPM II 0; C) curva ROC para SAPS II.

Finalmente, la coincidencia de capacidad predictiva fue estudiada mediante el método de concordancia de Bland-Altman. El análisis de los gráficos representados en las figuras 2 A y B permite comprobar que, en ambos casos, el IC al 95% es demasiado amplio (más de 80 puntos) y que en el caso de análisis de concordancia entre EPEC y SAPS II, más de un 5% de los puntos de coincidencia de los pares de predicciones están fuera del IC admitido. Podemos, pues, afirmar, que no existe concordancia entre las predicciones de mortalidad de EPEC y los otros dos métodos.

Figura 2. Análisis de concordancia predictiva mediante el test de Bland-Altman. A) Concordancia EPEC (estimación pronóstica en enfermos críticos)-MPM II 0; B) Concordancia EPEC-SAPS II.

DISCUSIÓN

Cuando el investigador interesado en la aplicación de la práctica de la teoría del pronóstico se enfrenta a un nuevo método de estimación pronóstica (en este caso de supervivencia de pacientes críticos atendidos en un Servicio de Medicina Intensiva), debe tener permanentemente presentes las condiciones que debe cumplir en teoría cualquier método de estimación pronóstica de supervivencia.

Entre ellas están: la relación lineal de la estimación (n-1 < n < n+1), la simplicidad de las variables utilizadas, la reproducibilidad de la estimación y la validación en muestra distinta de la utilizada para el diseño del sistema3,4. A estas condiciones relacionadas con la estrategia de diseño cabe añadir condiciones estrictamente de elaboración y estructuración matemática: una alta calibración, una alta discriminación y la posibilidad de que sus «prestaciones» (capacidad operativa de establecer un pronóstico) sean comprobadas en distintos ámbitos5. El anexo 2 ofrece las definiciones de calibración y discriminación.

En lo que se refiere a EPEC cabe destacar que algunas de estas condiciones no se cumplen en su descripción original, tanto en los aspectos de diseño (validación en muestra independiente) como en los de elaboración matemática (comprobación de prestaciones en distintos ámbitos). De ello nace la necesidad y el interés de esta aportación, y más cuando la simplicidad de diseño ofrece condiciones que pudieran hacer al método atractivo para su utilización en cualquier UCI.

La sencillez de elaboración de un método de estimación pronóstica debe apoyarse en la utilización de variables que puedan estar disponibles en cualquier ámbito de posible aplicación, con independencia de tecnologías y sofisticación de procedimientos de obtención; en este aspecto radica el principal capital potencial del método estudiado aquí. EPEC, al igual que otros métodos de estimación pronóstica de supervivencia de enfermos críticos, parte de esta premisa incuestionable. Ninguno de los sistemas más utilizados en la práctica (APACHE6,7, SAPS8,9, y los derivados del método MPM10,11) utilizan variables que estén alejadas de la disponibilidad más rutinaria. No por incluir la determinación de los niveles de hormona del crecimiento, o complejas elaboraciones matemáticas a partir de variables fisiológicas simples, se mejora la prestación de una estimación pronóstica.

Fiel a esta concepción EPEC no incorpora ninguna variable que pueda ser catalogada de sofisticada o difícil de obtener, y éste es, junto con una simplificación importante de los procedimientos de cálculo necesarios para su aplicación (anexo 1), su principal atractivo.

Pero no es éste su único valor intrínseco. Desde los trabajos de Dragsted12 se acepta que el tiempo de retraso del ingreso del paciente en UCI en situación crítica es determinante para el resultado final. Este tiempo puede ser considerado de una forma bivalente: el retraso en identificar la situación de riesgo vital (al que podríamos llamar «retraso fisiopatológico», ya que está relacionado con las alteraciones que determina este retraso en la identificación del problema) y otra forma que sería la del retraso asociado a la imposibilidad de aceptar el ingreso del paciente candidato a tratamiento en UCI, ya sea por falta de disponibilidad de camas o por cualquier otro motivo. A éste podría llamársele «retraso logístico».

El trabajo original de Padrón et al, que describe EPEC1, opta por esta segunda posibilidad, expresando este «retraso» en horas completas, y en nuestro conocimiento es el único sistema de estimación pronóstica de supervivencia que incorpora, como factor independiente, el retraso logístico, que en determinados centros puede tener un peso determinante.

De cualquier forma, y siguiendo este mismo hilo argumental, cabe pensar que de los dos retrasos considerados (el fisiopatológico y el logístico), es el primero el que se asocia a peores consecuencias y el que exige mayor esfuerzo para ser modificado, ya que el retraso que hemos llamado logístico depende, en última instancia, de un adecuado funcionamiento de la propia UCI, mientras que el primero exige un cambio de mentalidad y de política de oferta y demanda por parte del conjunto de la estructura asistencial del centro.

Dentro de las promesas ofrecidas por los nuevos diseños de estimaciones pronósticas no se han conseguido solventar los déficit de prestaciones, ya denunciados recientemente por Knaus13, y que pueden resumirse en los dos aspectos clásicamente establecidos como limitaciones de todos los modelos de estimación pronóstica disponibles: uno hace referencia a la limitación de exactitud, que en la literatura se cifra en alrededor de un error por cada 10 casos predichos, es decir, en un 10% de las predicciones. Esta limitación impide que la aplicación de los métodos predictivos de supervivencia pueda ser ascendida a niveles de criterio de decisión. Mientras exista una cierta incerteza ligada a la inexactitud (intrínseca) de predicción, las estimaciones pronósticas serán sólo instrumentos de trabajo en estudios de calidad4, pero no motivos de adopción de decisiones clínicas.

El otro consiste en la toma de decisiones asistenciales, ya que no se solventa el problema de las predicciones individuales frente a las de grupo. De hecho, ¿cómo puede interpretarse que un paciente tenga una probabilidad de sobrevivir (inversa del riesgo de muerte) de, digamos, 0,75? ¿Cuál es la traducción práctica para el paciente afecto de complicación perforativa secundaria a neoplasia intestinal, intervenido hace 12 horas y con un riesgo de muerte del 25%? Esta es la principal objeción a los instrumentos predictivos, que su utilización en pacientes concretos e individuales es sólo orientativa y no permite ningún tipo de decisión concreta.

A la luz de la existencia, de la persistencia deberíamos decir, de estas limitaciones deben justificarse todos los intentos destinados a refinar la capacidad pronóstica, y en este sentido los esfuerzos de todos los investigadores deben ser vistos con respeto y merecer el máximo de atención, en función de su promesa implícita. Pero este aspecto estimulante de búsqueda del instrumento más adecuado no debe olvidar las condiciones establecidas para la creación de nuevas estrategias predictivas, y de ahí nuestro interés en validar (en una muestra distinta e independiente de la utilizada para el diseño) EPEC.

Desde el punto de vista de la validación de un nuevo método de estimación pronóstica, y al estudiar sus «prestaciones» en una población distinta de la inicialmente utilizada para el desarrollo de método, la cuestión fundamental es establecer si el nuevo método «funciona» mejor que los disponibles hasta ese momento, y comparar las predicciones obtenidas con el método incógnita frente a las recogidas con otros sistemas perfectamente consolidados. En nuestro estudio se ha comparado la capacidad predictiva de EPEC con las de MPM II 0 y SAPS II.

Desde el punto de vista de la discriminación entre supervivientes y no supervivientes es evidente que la capacidad de EPEC es claramente superponible a la de los otros métodos. El cálculo de las áreas bajo las curvas ROC para cada uno de los tres métodos proporciona valores (figs. 1 A, B y C) cuantitativamente tan próximos, que es evidente que no existen superioridades de un método con respecto a otro.

Estas aparentes similitudes de capacidad pronóstica se ven comprometidas al analizar la calibración obtenida y realizar los cálculos de resolución de las tablas de contingencia construidas alrededor de distintas probabilidades de mortalidad. EPEC no permite analizar adecuadamente la calibración al no existir, por este método, una probabilidad de muerte superior al 50%, y a ello se debe añadir el análisis comparativo de la SMR frente a MPM II 0 y SAPS II. Mientras que estos métodos no ofrecen diferencias significativas entre ellos al establecer la comparación entre predicciones de mortalidad y mortalidad real, EPEC sí aporta diferencias significativas frente a los dos métodos, considerados aquí como gold standards.

En este mismo sentido debe interpretarse el resultado de los análisis de concordancia (test de Bland-Altman) realizados, que demuestran que no existen coincidencias suficientes entre las predicciones de EPEC y las de SAPS II o MPM II 0.

A la luz de estos resultados creemos adecuado afirmar que, en su estado actual, EPEC no sólo no ofrece ventajas tangibles frente a otros métodos de estimación pronóstica más introducidos en la práctica (MPM II 0 y SAPS II), sino que su capacidad de pronosticar adecuadamente el riesgo de muerte es más que discutible.

Como resumen de nuestro trabajo se puede afirmar que éste es más un ejercicio encaminado a analizar la adecuación metodológica de un sistema de predicción de mortalidad, que a establecer su posibles bondades (que no las presenta) frente a sistemas más habituales en la práctica.

AGRADECIMIENTOS Y CRÉDITOS

Aspectos parciales de este trabajo han sido presentados en el XXXIX Congreso Nacional de la Sociedad Española de Medicina Intensiva, Crítica y Unidades Coronarias (SEMICYUC), celebrado en Tarragona en junio de 2004; y en el Congreso anual de la European Society of Intensive Care Medicine (ESICM), celebrado en Berlín en octubre de 2004.

Declaración de conflicto de intereses

Los autores han declarado no tener ningún conflicto de intereses

Correspondencia: Dr. R. Abizanda i Campos.

Servei de Medicina Intensiva.

Hospital Universitario Asociado General de Castellón.

Avda. Benicàssim, s/n.

12004 Castellón. España.

Correo electrónico:

abizanda_ric@gva.es

rabizandac@terra.es

Manuscrito aceptado el 23-I-2006.