La interpretación de los resultados estadísticos es un elemento crucial para la comprensión de los avances en las ciencias médicas. Las herramientas que nos ofrece la estadística nos permiten transformar la incertidumbre y aparente caos de la naturaleza en parámetros medibles y aplicables a nuestra práctica clínica. La importancia de entender el significado y alcance real de estos instrumentos es fundamental para el investigador, para los financiadores de las investigaciones y para los profesionales que precisan de una actualización permanente basada en buena evidencia y ayudas a la toma de decisiones. Se repasan diversos aspectos de los diseños, resultados y análisis estadísticos, intentando facilitar su entendimiento desde lo más elemental a aquello que es más común pero no por ello mejor comprendido y aportar una mirada constructiva y realista, sin ser exhaustiva.
The appropriate interpretation of the statistical results is crucial to understand the advances in medical science. The statistical tools allow us to transform the uncertainty and apparent chaos in nature to measurable parameters which are applicable to our clinical practice. The importance of understanding the meaning and actual extent of these instruments is essential for researchers, the funders of research and for professionals who require a permanent update based on good evidence and supports to decision making. Various aspects of the designs, results and statistical analysis are reviewed, trying to facilitate his comprehension from the basics to what is most common but no better understood, and bringing a constructive, non-exhaustive but realistic look.
La investigación clínica es un medio indispensable para la evolución del conocimiento científico y su aplicación a la práctica clínica habitual, para ofrecer a los pacientes las mejores oportunidades para recuperar o mejorar su salud, entendida como tiempo y calidad de vida1.
Para ello necesitamos contar con herramientas que nos permitan investigar, describiendo la realidad biológica, facilitando la comprensión de su comportamiento, y permitiendo la manipulación a través de experimentos para establecer asociaciones entre un estímulo (medicamento, técnica quirúrgica,…) y un resultado de interés.
Las técnicas estadísticas son modelos matemáticos que requieren determinados conocimientos para su interpretación2,3. Sin una adecuada comprensión, la extrapolación de resultados de los estudios puede ser inútil o peligrosa. El esfuerzo de entendimiento es imprescindible si se desea estar actualizado en los avances científicos desde un compromiso ético4. Además, dada la enorme producción científica existente, favorecida por la necesidad de publicar para avanzar profesionalmente, se exige saber interpretar los resultados estadísticos para distinguir lo importante de lo accesorio, desarrollar un espíritu crítico5 y valorar las implicaciones para nuestra práctica clínica e investigadora.
El objetivo de este trabajo es ofrecer una visión general de la interpretación de los análisis estadísticos más frecuentes, haciendo hincapié en las limitaciones y los posibles errores (tabla 1), para facilitar una adecuada comprensión de los mismos. La información podrá ser básica o más compleja, no exhaustiva pero siempre necesaria, e irá referenciada a su uso en la investigación del paciente crítico.
Errores frecuentes de interpretación de resultados estadísticos
| Errores frecuentes de interpretación | |
|---|---|
| Significativo igual a importante | La significación estadística es un término matemático. La importancia clínica debe valorarse por el impacto real de los resultados |
| No significativo implica igualdad | Las diferencias no significativas no permiten establecer la equivalencia de manera directa, aunque un intervalo de confianza de la diferencia suficientemente pequeño estimula a no seguir buscando diferencias |
| Correlación equivale a concordancia | La correlación es una medida de relación lineal entre variables cuantitativas, mientras que la concordancia mide el acuerdo en la medición de variables |
| Cuanto más pequeña es la p, mayor asociación existe | La p hace referencia a la probabilidad de que la diferencia encontrada se deba al azar del muestreo, pero no mide la fuerza de la asociación |
| El intervalo de confianza incluye el valor real de la variable | El intervalo de confianza expresa la confianza en que repitiendo el experimento, en un 95% de veces el resultado estará incluido en ese intervalo. Pero no implica que el valor poblacional esté en dicho intervalo |
| Una diferencia no significativa se arregla con más muestra | Podemos incrementar la muestra hasta obtener una p significativa, pero ello no dará relevancia a los hallazgos |
| Odds ratio y riesgo relativo es lo mismo | La odds ratio se utiliza en estudios de casos y controles y análisis multivariantes, y mide proporción de riesgos entre tener y no tener el factor. El riesgo relativo se obtiene en estudios de cohortes y ensayos clínicos, y permite obtener la razón de incidencias reales. La odds ratio es una aproximación al riesgo relativo |
| Gran tamaño de muestra equivale a más representatividad | La representatividad de una muestra no depende del tamaño sino de los criterios de selección |
| «Hemos encontrado diferencias, pero no son significativas» | Siempre se encuentran diferencias (si es lo que se busca). Si la p no es significativa, solo podemos decir que no descartamos que sean por azar. Mejor entonces no contarlo |
Los estadísticos de resumen permiten visualizar las características de la distribución de los datos ayudando a sintetizar la dimensión de cambio de una variable, y son conceptos básicos de estadística. La media aritmética es la suma de cada uno de los valores dividido por el número total de sujetos de una población. Se afecta por la existencia de valores extremos, por lo que no es adecuada para distribuciones poco uniformes6, como la estancia en UCI. La media recortada elimina los valores extremos, y la moda corresponde al valor más frecuente dentro de la distribución, pero la utilidad de ambas es limitada.
La varianza es un indicador que permite establecer la separación de un conjunto de datos respecto a su media aritmética, aunque solemos usar la desviación estándar (típica, standard deviation [DE]) como la raíz cuadrada de la variancia, expresándose en las mismas unidades de la variable7. La DE refleja la dispersión de la distribución, y una DE superior a la media suele indicar una distribución asimétrica (cuando el número de casos es mayor en valores altos o bajos, como la estancia en UCI). Si es una distribución normal, nos dará los valores entre los cuales se encontrará el 68% (±1DE), el 95% (±2DE), o el 99,7% (±3DE) de los datos. Este es el origen de la popular expresión media±DE, aunque se prefiere hablar de media (DE).
Cuando la distribución de la variable es asimétrica, utilizamos medidas basadas en ordenaciones. La mediana es el valor central obtenido tras ordenar los valores, y los cuartiles, deciles o percentiles resultan de dividir la muestra ordenada en 4, 10 o 100 partes iguales. La mediana coincide con el 2.o cuartil, el 5.o decil y el percentil 50. En estos casos, las medidas de dispersión preferidas son los percentiles 25 y 75 o la diferencia entre ambos, que se denomina rango intercuartílico (interquartile range [IQR]). No es lo mismo que el rango de una variable, que indica los valores menor y mayor. La estancia en UCI o los días de ventilación mecánica son variables de distribución asimétrica que preferimos representar por mediana y percentiles 25-75 o con el rango intercuartílico8.
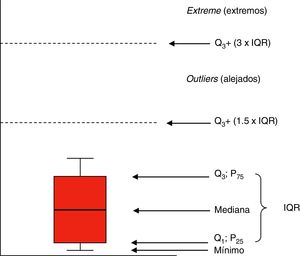
Representaciones gráficasLas distribuciones de variables cuantitativas suelen representarse mediante histogramas (diagramas de barras) o gráficos de dispersión (diagramas de puntos). Los diagramas de caja o boxplots (fig. 1) resumen bien la distribución de una variable. La caja está limitada de abajo a arriba por los cuartiles Q1 y Q3, con la mediana en el centro. Las alas de la caja contienen hasta el valor mínimo por debajo y hasta el límite de Q3 más 1,5 veces el IQR. Los valores por encima de este margen son valores alejados (por encima de Q3+1,5×IQR) y extremos (por encima de Q3+3×IQR).
Prevalencia e incidenciaPrevalencia es la proporción de casos de una población que presenta un determinado rasgo o enfermedad. La prevalencia puede ser puntual o de periodo, cuando se analiza un lapso de tiempo de t0 a t1 y se cuenta la población a la mitad del intervalo. Los estudios del registro ENVIN-UCI son un ejemplo de este último tipo de diseño9. Los estudios de prevalencia evalúan tendencias globales y permiten generar hipótesis, pero no permiten establecer asociaciones causales.
La incidencia es el número de nuevos casos de una enfermedad o rasgo que aparecen en una población a lo largo de un periodo de tiempo. La incidencia acumulada corresponde a la proporción de pacientes en riesgo libres de enfermedad que desarrollan la enfermedad en un periodo de tiempo. La tasa de incidencia (o densidad de incidencia [DI]) es el número de casos nuevos en un periodo de tiempo, dividido por la suma de unidades de tiempo en riesgo de cada uno de los sujetos expuestos.
Por ejemplo, en una población de 200 pacientes críticos intubados al menos 48h aparecen 16 neumonías asociadas a la ventilación mecánica (NAVM) en un periodo de seguimiento de un mes. El riesgo o incidencia acumulada de NAVM será de 16/200=8% para cada individuo, o de 8 por 100 pacientes ventilados al mes. En los pacientes críticos, las medidas de incidencia acumulada pueden ser poco informativas dado que los factores de riesgo cambian y hay pérdidas (fallecidos o que dejan de tener el factor de riesgo, como la ventilación mecánica). En ese caso podemos utilizar el modelo actuarial, que tiene en cuenta estas pérdidas, o la DI. Este último es el indicador que utilizamos para las infecciones relacionadas con dispositivos (ventilación mecánica, catéteres). Se mide en unidades recíprocas de tiempo (6 NAVM por 1.000 pacientes día de ventilación mecánica, 3 infecciones relacionadas con catéter por 1.000 pacientes día de catéter). La valoración de las unidades de tiempo asociadas al riesgo puede tener importancia, al no incorporar efectos acumulativos producidos por el mantenimiento de los factores. No es lo mismo 500 pacientes con 3 días de ventilación mecánica que 300 pacientes con 5 días, o un paciente con varios catéteres y un total de 6 luces que un paciente con un catéter de 2 luces, aunque los denominadores sean iguales. Por convenio, se suele considerar la suma total de días en ventilación mecánica y la suma de total de días con catéter10.
Medidas de asociaciónPermiten la cuantificación de la relación existente entre 2 variables. Su objetivo es establecer si existe asociación entre una exposición o rasgo y una enfermedad, aunque esto no presuponga causalidad. Estas medidas establecen si la frecuencia de una característica (enfermedad) es diferente entre los expuestos a una determinada variable.
Diferencia absoluta de proporciones. Se denomina diferencia de riesgos (risk difference), riesgo atribuible (attributable risk), exceso de riesgo (excess risk) o reducción absoluta de riesgos (absolute risk reduction). Expresa cuánto se incrementa o disminuye el riesgo de un determinado evento según el grupo al que pertenezca. Es una medida absoluta que ofrece una información limitada, pues una reducción del 1% puede ser muy importante si el riesgo basal es del 2%, pero insignificante si el riesgo inicial es del 30%.
Odds de enfermedad. La odds es un término anglosajón utilizado en apuestas, y significa cuánto más probable es que se produzca un resultado que otro. Por ejemplo, si la probabilidad de que sobreviva un paciente es del 75% y la de que fallezca es de un 25%, la odds de supervivencia sería 75%/25% de 3 a 1, o de 3 para simplificar. Esto es, la probabilidad de supervivencia es 3 veces superior a la de fallecimiento.
Diferencia relativa de proporciones. También llamada diferencia relativa de riesgos (relative risk difference [RRD]), o reducción relativa de riesgo (relative risk reduction [RRR]). Es la diferencia de riesgos o incidencias dividida entre la incidencia en el grupo de comparación. Trata de explicar cuánto varía el riesgo al cambiar de grupo de comparación. Suele utilizarse para magnificar la cuantía de los efectos. Por ejemplo, pasar de una incidencia del 0,99% al 0,75% puede ser clínicamente más o menos relevante, pero una reducción de riesgo relativo del 24% (mismos datos) suena mucho más impactante, sobre todo si no se incluye el intervalo de confianza de dicha estimación11.
Razón de proporciones. Se denomina riesgo relativo o razón de riesgos (relative risk, risk rate [RR]). Es el indicador con más éxito, y se calcula como el cociente de la incidencia en los expuestos frente a la incidencia en los no expuestos. Su interpretación es cuántas veces se incrementa (o reduce) el riesgo de presentar un evento dependiendo de la exposición. Un RR mayor de 1 implica un incremento del riesgo, un efecto nulo si es igual a 1 y una reducción de riesgo si es menor de 1. Al ser una medida relativa, debe ir acompañada de los datos de incidencia absoluta, para poder calibrar la relevancia clínica del efecto. Una mortalidad del 0,03% frente a una mortalidad del 0,01% generaría un RR de 3. Sin embargo, el impacto clínico de esta asociación puede no ser relevante. Los RR por debajo de 1 pueden ser difíciles de interpretar. Un RR de 0,20 no equivale a una reducción del riesgo en un 20%, sino a 1/0,20 un riesgo 5 veces menor.
En estudios longitudinales y ensayos clínicos existe una medida denominada número necesario a tratar (NNT). Permite conocer a cuántos sujetos habría que aplicar un determinado tratamiento para conseguir un resultado positivo adicional o para evitar un resultado negativo. Se calcula con el inverso de la diferencia absoluta de incidencias.
Razón de odds. Se denomina odds ratio (OR), y no tiene una traducción inequívoca en español. Su interpretación depende del contexto del diseño del estudio en el que se utilice. En estudios de casos y controles, no se conoce la incidencia real de la enfermedad en los no expuestos, porque no se sigue toda la población, sino que se selecciona una muestra representativa de la misma. Ello no permite conocer el RR al no disponer de la incidencia en los no expuestos. Sin embargo, sí podemos saber la odds de exposición al factor de riesgo en los expuestos y en los no expuestos: es decir, cuánto más probable es que un enfermo esté expuesto y cuánto más probable es que un no enfermo lo esté. El cociente de estas odds es lo que denominamos OR en los estudios de casos y controles. Su interpretación es una estimación de la razón de incidencias (RR) en la población original, siempre que la selección de los controles haya sido independiente de la exposición.
Intervalos de confianzaCualquier medida que se realice con una muestra de sujetos es una estimación de la medida real en la población general, que es lo que deseamos conocer. Cuando seleccionamos una muestra, esperamos que sea representativa de la población, y utilizaremos criterios de inclusión y exclusión que faciliten la realización del estudio concreto pero que no generen excesivas diferencias con la población objetivo, para poder generalizar los resultados.
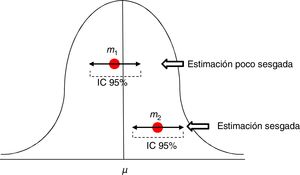
Para valorar la estimación de una medida utilizamos los intervalos de confianza (IC), habitualmente al 95%. El IC al 95% no equivale a decir que la medida se encuentra en la población real en ese intervalo con un 95% de probabilidades. El significado del IC al 95% es que tenemos confianza en que el método utilizado nos dará muestras que en un 95% de los casos generarían un estimador incluido en ese intervalo. Pero no implica que el indicador en la población real esté incluido en ese intervalo, podrá estarlo o no (fig. 2).
Estimaciones de una media con su intervalo de confianza al 95%. La primera m1 es una estimación poco sesgada, mientras que la segunda m2 está sesgada, y su intervalo de confianza nos informa de que con un 95% de confianza, si repetimos el experimento obtendremos un estimador en dicho intervalo, pero no incluirá el de la media μ real.
La regresión lineal es el procedimiento por el cual podemos establecer una relación lineal (y=a+bx) en el comportamiento de 2 variables. Ello se aprecia gráficamente cuando se genera una nube de puntos con las parejas de las variables que se acerca a una línea recta, y permitiría definir los valores de una variable en función de la otra.
La correlación es la asociación lineal entre 2 variables que son independientes, y se establece como una simetría en el comportamiento de ambas. Es importante resaltar que la correlación no implica la existencia de causalidad, sino que existe alguna asociación con una variable intermedia entre ambas12.
Para medir la correlación entre 2 variables utilizamos la covariancia, o su estandarización que es el coeficiente de correlación r de Pearson. Este índice precisa que la distribución de las variables sea normal y varía entre –1 (correlación negativa) y +1 (correlación positiva). Cuando su valor es próximo a 0, no existe correlación lineal. En los casos en los que la distribución no sea normal puede utilizarse el coeficiente de correlación de Spearman o el de Kendall, basados en ordenaciones, que permiten detectar correlaciones no lineales.
Para interpretar la correlación no debe olvidarse que el coeficiente r de Pearson mide asociación lineal, pero puede haber correlaciones no lineales entre variables. Es importante tener medidas no sesgadas y comprobar el impacto de los valores extremos. Las correlaciones deben plantear alguna lógica de asociación, evitando dar por buenas asociaciones espurias, aquellas que relacionan la parte con el todo (APACHEII con disfunción renal), o el uso de variables con valores calculados (pH y exceso de bases). Otro uso incorrecto y frecuente es utilizarla como análisis de concordancia entre diferentes herramientas para medir una variable.
Los estudios de fiabilidad analizan la variación en la medición de una variable, bien con un instrumento de medida y un mismo observador (intraobservador) o varios observadores (interobservador) o la concordancia entre 2 instrumentos de medición13. Estos estudios son frecuentes en medicina crítica, estimando parámetros invasivos a través de medios no invasivos. La concordancia entre mediciones en variables cualitativas utiliza el índice kappa, que mide la tasa de aciertos entre observadores restando el acuerdo previsible por el azar, y se mueve entre 1 (máxima concordancia) y valores que pueden ser negativos. Se estima que valores de índice kappa por encima de 0,6 indican concordancia buena y por debajo de 0,4 indican concordancia débil. Para variables politómicas u ordenadas (grados de insuficiencia cardiaca, p.ej.), se usa el índice kappa ponderado14. El índice kappa debe evitarse en agrupaciones cualitativas de variables cuantitativas.
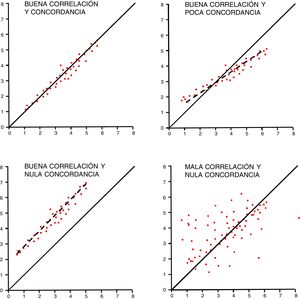
La concordancia entre variables cuantitativas se mide con el coeficiente de correlación intraclase (R), que analiza conjuntamente la varianza de los sujetos, del instrumento de medición y el propio error de medida15. Se estima por convención que para hablar de buena concordancia, debe ser superior a 0,75. Un método gráfico sencillo para comprobar la concordancia en variables cuantitativas es el método de Bland y Altman, que muestra las diferencias individuales entre las medidas en relación con su media16. Debe recordarse que, para estos estudios, la correlación no es buen método de análisis aunque pueda coincidir con el coeficiente R (fig. 3).
Validez y precisión de los estudiosLa validez de un estudio puede definirse como la consistencia interna y externa de los resultados, que generan confianza en que los datos obtenidos representan la realidad que queremos observar. Si realizamos un estudio de pacientes críticos sépticos y utilizamos criterios no actualizados de la sepsis, se compromete la consistencia de los resultados y por tanto la validez interna. Si no se incluyen pacientes inmunocomprometidos, la muestra puede no ser representativa de la población global de pacientes con sepsis, por lo que se ve comprometida la validez externa. La validez interna es un requisito indispensable para un estudio, mientras que la validez externa facilita la posibilidad de generalizar los resultados obtenidos. Es necesario tener cuidado con los sesgos de selección (tabla 2). Uno de ellos es considerar el enfermo crítico como un tipo de enfermo y no como una situación clínica que se produce en diferentes enfermedades. Puede haber sesgos de información por la diferencia de registros entre la UCI y el ingreso previo, pudiendo generar problemas en la valoración de variables de interés entre pacientes con diferente estancia previa17.
Sesgos frecuentes en investigación clínica
| Sesgos | ||
|---|---|---|
| Selección | Mala selección del grupo control | Los criterios de selección para controles influyen en la variable pronóstica |
| Sesgo de Berkson | En casos y controles hospitalarios, cuando la probabilidad de hospitalización es mayor en los casos que en los controles, pudiendo detectar asociaciones inexistentes | |
| Sesgo del voluntario | La autoselección puede generar diferencias en la exposición o la enfermedad | |
| Sesgo de adelanto diagnóstico | Una prueba muy sensible diagnostica una enfermedad en fases latentes o incipientes, sobreestimando la incidencia | |
| Sesgo de prevalencia-incidencia | Si se analizan solo casos prevalentes, se verán casos tardíos de la enfermedad, y los casos graves y fulminantes pasarán desapercibidos | |
| Pérdidas de seguimiento | La causa de las pérdidas está relacionada con la exposición y la enfermedad | |
| Supervivencia selectiva | Se estudian casos prevalentes y la supervivencia está relacionada con la exposición | |
| Detección | El medio de detección de la enfermedad varía según esté presente la exposición | |
| Muestra no representativa | Criterios de selección de muestra inadecuados a la población que se desea estudiar | |
| Información | Error de clasificación no diferencial | La clasificación errónea de sujetos se reparte por igual en ambos grupos. Genera infraestimación de la asociación |
| Error de clasificación diferencial | La clasificación errónea de sujetos es diferente en ambos grupos. Puede generar infraestimación o sobreestimación de la asociación. El más conocido es el sesgo de memoria | |
| Sesgo de confusión | Existe una variable confundidora relacionada con la exposición y la enfermedad que distorsiona el efecto que deseamos medir | |
La precisión de un estudio es el margen de error con el que se obtienen los resultados. Depende en gran medida, pero no solo, del tamaño de la muestra. Hay diseños y modos de registro y análisis más eficientes para conseguir mayor precisión, como utilizar variables cuantitativas en vez de cualitativas o realizar análisis de supervivencia en vez de analizar el resultado como una variable dicotómica.
Pruebas de significaciónLas pruebas de significación estadística obtuvieron notoriedad con Fisher, quien con un abordaje bayesiano planteó este modelo de análisis: dada como cierta una hipótesis nula H0 (ausencia de diferencias entre 2 tratamientos), se realiza un experimento que ofrece unos resultados, y se calcula la probabilidad p de haber obtenido dichos resultados considerando que H0 fuera cierta. Una p muy pequeña obligaría a buscar alternativas a H0, aunque no la rechazaría.
Casi al mismo tiempo, Neyman y Pearson plantearon un método alternativo, basado en la existencia de 2 hipótesis —la hipótesis nula H0 (ausencia de diferencias) y la alternativa H1 (existen diferencias)— y se definía un error tipoI (cometido al dar por válida la H1 siendo cierta la H0) y un error tipoII (dar por válida la H0 siendo cierta la H1). El experimento iba encaminado a decidirse por una de ellas en función de la probabilidad de cometer el error tipoI (riesgo α) o el error tipoII (riesgo β).
Hoy día se trabaja habitualmente en un método combinado18, definiendo una hipótesis nula H0 y proyectando un experimento que permita detectar una cierta diferencia. Posteriormente se calcula la probabilidad p de haber obtenido dichos resultados considerando cierta la H0. Si la p es pequeña, se rechaza la validez de la H0 (es decir, hay diferencias), y si no lo es, no se rechaza, pero tampoco se acepta. Es decir, que la ausencia de significación estadística en un ensayo no se interpreta como equivalencia terapéutica19.
La habitual obsesión de los investigadores por obtener p<0,0520 se basa en un convenio general, originado en Fisher21, que planteaba que encontrar un resultado por azar no más de una vez de cada 20 ensayos podría considerarse significativo. Sin embargo, la buscada p depende de la magnitud de la diferencia, pero más del tamaño de la muestra, y basta incrementarlo para obtener resultados «estadísticamente significativos»22. Al investigador corresponde interpretar si un resultado estadísticamente significativo puede considerarse clínicamente relevante23,24. Un reciente artículo de NEJM, basado en el análisis de 49.331 ingresos urgentes por sepsis25, demuestra estadísticamente que el riesgo de muerte hospitalaria se incrementa un 4% (OR de 1,04 [IC95%: 1,02-1,05]; p<0,001) por cada hora si no se completa el paquete de medidas (hemocultivos, antibioterapia y fluidos) antes de las 3h. En la tabla comparativa se muestra cómo la diferencia entre completar el paquete de medidas antes de 3h y entre 3 y 12h pasa de un 22,6% de mortalidad a un 23,6%. Estos porcentajes no se interpretarían como diferentes en cualquier estudio con un número asequible de pacientes, pero aquí han obtenido una p significativa gracias al enorme tamaño de la muestra. La interpretación de la importancia de ese incremento de mortalidad corresponde a los clínicos, y por supuesto no depende del valor de p. Nunca hay que olvidar que el valor de la p no mide la magnitud del efecto.
Los análisis univariantes analizan una variable en diferentes grupos de individuos con una característica, como tener un factor de riesgo o recibir un tratamiento. Se utilizan test que podrán aplicarse en variables cuantitativas si las distribuciones son normales (t de Student para 2 muestras, ANOVA para varias muestras), o no normales (U de Mann-Whitney para 2 muestras, Kruskal-Wallis para varias muestras, Wilcoxon para medidas repetidas). Para determinar si una variable sigue una distribución normal, se utilizan los test de Kolmogorov-Smirnov y Shapiro-Wilk. Para variables cualitativas usaremos la chi cuadrado de Pearson o el test de Fisher.
Recientemente, una corriente creciente de expertos en estadística apoya el fomento de la estadística bayesiana como herramienta de aproximación más adecuada a la realidad de la investigación clínica26.
Interpretación de análisis multivariantesSon técnicas que permiten estudiar la interrelación matemática de múltiples variables en un conjunto de datos. La aparición de programas estadísticos con potentes analizadores ha popularizado su uso y dota a sus resultados de mayor poder de convencimiento. Sin embargo, la complejidad de los análisis multivariantes no reside en las herramientas matemáticas necesarias, sino en la consistencia de las hipótesis planteadas, en la adecuada selección de variables, en la aplicación de las técnicas apropiadas y en la interpretación prudente de las mismas.
Un planteamiento metodológico adecuado incluye caracterizar la población de estudio, las variables de análisis, y la asociación a investigar, definiendo los criterios de inclusión para obtener una muestra representativa de dicha población. Al interpretar un análisis multivariante, más importante que comprender el significado de los resultados lo es conocer si las variables relevantes han sido incluidas en el modelo. El análisis multivariante no solucionará el hecho de no haber incluido un factor importante en la asociación buscada. Por el contrario, la inclusión de muchas variables no hace mejor al modelo. Se recomienda que existan al menos 10 casos incidentes por cada variable incluida27. La robustez y el ajuste del modelo obtenido son muy relevantes, y pueden evaluarse por test como el de bondad del ajuste de Hosmer-Lemeshow (aunque tiene sus críticas al buscar la «no significación»), el -2 log de verosimilitud (-2LL), que es menor cuanto más se ajusta el modelo a los datos, y la R2 de Nagelkerke, que estima la proporción de la variación de la variable explicada por el modelo.
La asociación entre variables determinada por análisis multivariante no implica una relación de causalidad. Los clásicos criterios de causalidad de Bradford Hill no dependen del resultado matemático, sino del sentido común científico28 (tabla 3). Es imprescindible ser prudentes en la interpretación de resultados estadísticamente significativos, que pueden tener una relación espuria con la variable independiente. Estos métodos ayudan a valorar las variables confundidoras que dificultan el establecimiento y la comprensión de la causalidad, pero deben ser utilizadas de una manera dirigida en el análisis29.
Criterios de causalidad de Bradford Hill
| Criterios de causalidad | |
|---|---|
| Fuerza de asociación | A mayor fuerza de asociación, mayor causalidad |
| Criterio temporal | El efecto debe ser posterior a la causa |
| Efecto dosis-respuesta | A mayor dosis, mayor respuesta |
| Consistencia | Los resultados deben ser reproducibles |
| Plausibilidad biológica | Debe haber alguna hipótesis biológica razonable que sustente la asociación |
| Especificidad en la asociación | Una causa produce un efecto |
| Evidencia experimental | La hipótesis se demuestra experimentalmente |
| Analogía | Causas análogas producen efectos análogos |
La regresión múltiple intenta establecer una relación a través de una ecuación, normalmente lineal, entre los diferentes valores de variables cuantitativas. Busca una asociación matemática mediante una función entre el valor de una variable (dependiente) y el valor de otras (independientes). En cuidados intensivos, puede utilizarse en el cálculo indirecto de un valor de interés (gradiente alvéolo-arterial de oxígeno), en función de los valores de otras variables obtenidos por medios no invasivos (PaO2/FiO2, la PEEP, el APACHE IV y el SOFA)30. Los coeficientes generados permiten conocer cómo se modifica la variable dependiente en función de los valores de las variables independientes.
Regresión logísticaEstudia la relación entre variables independientes cualitativas o cuantitativas y una variable independiente cualitativa, habitualmente dicotómica, como por ejemplo la mortalidad. Las OR generadas para las variables independientes expresan cuánto más probable es que se produzca un determinado valor en la variable dependiente en función del valor que esta tome. Por ejemplo, si un estudio demuestra una asociación entre la inadecuación de tratamiento antibiótico empírico y la mortalidad a los 30 días por sepsis con una OR de 2, se interpreta que el riesgo de muerte a los 30 días se multiplica por 2 en los pacientes con sepsis y con antibioterapia empírica inadecuada. La caracterización de la muestra escogida y la selección de variables son fundamentales para valorar el impacto de otras variables que pueden generar confusión o interacción en el modelo. Las variables de confusión son variables externas a la relación, anteriores a la exposición y relacionadas con la exposición y la enfermedad. Producen sesgos en la estimación de un efecto, pudiendo generar un efecto falso, enmascarar un efecto real o incluso invertirlo, y se deben a una desigual distribución en los grupos de riesgo. En nuestro ejemplo, si la muestra escogida contiene una proporción elevada de sepsis quirúrgicas, el impacto de la antibioterapia empírica inadecuada será mucho menor que si la mayor parte de las sepsis son médicas31. Las interacciones se producen cuando hay variables que cambian la intensidad o el sentido de la relación entre el factor de riesgo y el efecto. La interacción no significa confusión, pues la distribución en los grupos de riesgo no es diferente.
Los análisis multivariantes de regresión logística son también una herramienta para la generación de escalas de puntuación para estimar prospectivamente la probabilidad de presentar un evento. Los estimadores beta generados por el modelo logístico, a partir de los cuales se calculan las OR, son utilizados para asignar puntuaciones a determinados valores de las variables, y con ellos generar una puntuación que permite calcular el riesgo para un paciente concreto32. Este es el caso de escalas pronósticas como APACHE, MPM, o SAPS. No lo es, sin embargo, en el caso de SOFA o el Lung Injury Score, aunque después se haya validado su asociación con la mortalidad33.
Regresión con datos de supervivenciaEl análisis básico de supervivencia se realiza con el método de Kaplan-Meier, cuya función de supervivencia determina la probabilidad de supervivencia pasado un tiempo t. Se pueden comparar curvas con el método de log rank (Mantel-Cox), pero este método no permite analizar otras variables asociadas.
El modelo de regresión de Cox permite establecer la asociación entre variables independientes y otra variable dependiente del tiempo, la supervivencia. La supervivencia estadística no alude estrictamente al tiempo transcurrido hasta la muerte, sino al tiempo libre del evento objeto del estudio. Los estimadores que genera este modelo se denominan tasas de riesgo (hazard rate o ratio [HR]), y su interpretación es en cuánto se incrementa la tasa instantánea de riesgo cuando la variable se incrementa en una unidad. La interpretación de los HR es diferente a las OR de la regresión logística34. La OR es una estimación del incremento de riesgo de un desenlace independiente del tiempo, mientras que las HR son incrementos de riesgo en función de la unidad de tiempo. Por ello, los resultados de estas técnicas no son intercambiables. La regresión de Cox necesita asumir que las variables de riesgo analizadas estarán presentes durante todo el tiempo de observación para ejercer su influencia. Esto es asumible para la diabetes o la edad, pero no para otras variables medidas puntualmente, como el APACHEII al ingreso o la reanimación de la sepsis. Aun así, es una técnica en auge35, que se ajusta bien a las necesidades de análisis de supervivencia en pacientes críticos.
Interpretación de resultados de pruebas diagnósticasLas herramientas para valorar la capacidad diagnóstica de las pruebas son sencillas, pero deben ser claramente aplicadas. La sensibilidad es la proporción de sujetos que presentan enfermedad con el test positivo. La especificidad es la proporción de sujetos no enfermos con el test negativo. Estos valores son independientes de la prevalencia de la enfermedad, pero varían con la gravedad de presentación. La sensibilidad y la especificidad parten de sujetos en los que ya se conoce que son o no enfermos, y catalogan la prueba en función de su acierto. En el proceso asistencial se utilizan más los valores predictivos, que parten de los resultados de los test para determinar la probabilidad de enfermedad. El valor predictivo positivo (VPP) determina la proporción de sujetos con test positivo que están realmente enfermos. El valor predictivo negativo (VPN) define la proporción de sujetos con el test negativo que no tienen la enfermedad.
Los valores predictivos dependen directamente de la prevalencia de la enfermedad en la población a la que se aplica. Esto es la probabilidad pretest, y condiciona los resultados de estos indicadores. Por ejemplo, el VPP de la procalcitonina para infección en una población de pacientes de consultas externas es diferente respecto a una población de pacientes de urgencias o de cuidados intensivos36. Otra forma de analizar los resultados de una prueba diagnóstica es mediante los cocientes de probabilidad (likelihood ratios). El cociente de probabilidad positivo significa cuánto más probable es que la prueba sea positiva en un enfermo frente a que lo sea en un no enfermo. Esto equivale al cociente entre sensibilidad y 1–especificidad. El cociente de probabilidad negativo es inverso al positivo, y significa cuánto más probable es que la prueba sea negativa en un no enfermo frente a que sea negativa en un enfermo. Los cocientes de probabilidad son independientes de la prevalencia, y ayudan en la práctica clínica.
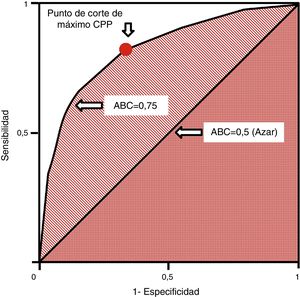
Las curvas ROC (receiver operating characteristics) se utilizan en pruebas cuantitativas y a cada valor o intervalo de resultados se le puede asignar una sensibilidad y especificidad para el diagnóstico de la enfermedad. Ello permite construir una curva a partir de pares de sensibilidad y 1–especificidad, lo que equivale a los cocientes de probabilidad positivos37. Se miden con el área bajo la curva (ABC [AUC, en inglés]), que se interpreta como la probabilidad de que al seleccionar un individuo enfermo y otro sano de manera aleatoria, el enfermo tenga un valor que sea diagnóstico frente al sano. La diagonal de la curva representa un área de 0,5 con una probabilidad del 50% de clasificación correcta, lo que equivale al azar. Por ello, una curva ROC que se acerque a la diagonal muestra una prueba diagnóstica de escaso valor. Las curvas ROC permiten establecer los puntos de corte de máxima sensibilidad y especificidad para una determinada prueba (fig. 4). Asimismo, se pueden comparar las AUC mediante test no paramétricos como el test de DeLong.
Curva ROC. Generada por parejas de sensibilidad y 1–especificidad. El punto de corte de máxima sensibilidad y especificidad puede establecerse por el mayor cociente de probabilidad positivo.ABC: área bajo la curva; CPP: cociente de probabilidad positivo; ROC: receiver operating characteristics.
Las herramientas estadísticas deben servir para mejorar nuestra capacidad de comprensión de la realidad biológica y de la respuesta ante nuestras intervenciones. La utilización e interpretación adecuadas son fundamentales para mejorar la salud de los pacientes.
Conflicto de interesesLos autores declaran no tener conflictos de interés relacionados con el objeto de este artículo.