INTRODUCCIÓN
Los modelos de predicción de mortalidad hospitalaria se emplean de forma habitual en los enfermos que ingresan en la Unidad de Cuidados Intensivos (UCI). Estos modelos se utilizan para evaluar los resultados de cada UCI y son necesarios, entre otras finalidades, para estratificar correctamente los enfermos a la hora de participar en ensayos clínicos controlados1. Entre otros, el sistema MPM II (Mortality Probability Model) es uno de los modelos más utilizados en nuestro entorno. Este sistema se desarrolló utilizando la metodología de regresión logística (RL) con una gran base de datos que incluía 19.124 pacientes dentro de un amplio estudio europeo y norte-americano (European/North American Study of Severity Systems)2.
El sistema MPM II consta de dos partes: el modelo Admisión, que incluye las variables tomadas en el momento de admisión en UCI, y el modelo 24-horas, con variables registradas durante las primeras 24 horas de ingreso en la unidad. Este sistema ha sido evaluado en diferentes grupos de pacientes y ha mostrado ser una buena herramienta para la estratificación de riesgo3.
La fiabilidad de un modelo de predicción se mide determinando su habilidad de distinguir los pacientes supervivientes y los que fallecerán (discriminación), y el grado de correspondencia entre la mortalidad observada y la esperada (calibración)4. En la práctica clínica, la aplicación de un modelo determinado en una UCI concreta puede mostrarnos una falta de precisión debida, en la mayoría de ocasiones, a una pérdida de calibración. La utilización de modelos específicos para cada UCI se hace necesaria si queremos valorar aspectos de control de calidad5. En nuestra UCI, por las características propias que nos alejan de las condiciones medias de la población que sirvió para confeccionar el MPM II, necesitamos adaptar o reajustar este modelo para conseguir una correcta estratificación del riesgo de muerte en nuestros pacientes. Para reajustar este modelo, podemos emplear metodología estadística, basada en RL, o también utilizar como alternativa un modelo basado en redes neuronales artificiales (RN).
Las RN constituyen una alternativa a los modelos basados en técnicas estadísticas. Las RN aportan una metodología general como modelos de predicción de resultados que son función de las correspondientes variables de entrada. Mediante un proceso de aprendizaje (llamado también entrenamiento) las RN desarrollan la capacidad de predicción de la variable resultado, en nuestro caso la probabilidad de mortalidad hospitalaria, a partir de un grupo de casos suficientemente amplio. Una vez entrenada correctamente la RN adquiere la capacidad de generalización: es capaz de enfrentarse a casos nuevos (no utilizados en la fase de aprendizaje) y dar resultados correctos6. Según los resultados publicados, las RN son entre un 5%-10 % más precisas que otras técnicas estadísticas, ya que no trabajan con restricciones de modelos lineales y son capaces de incorporar automáticamente las relaciones entre las variables predictoras7.
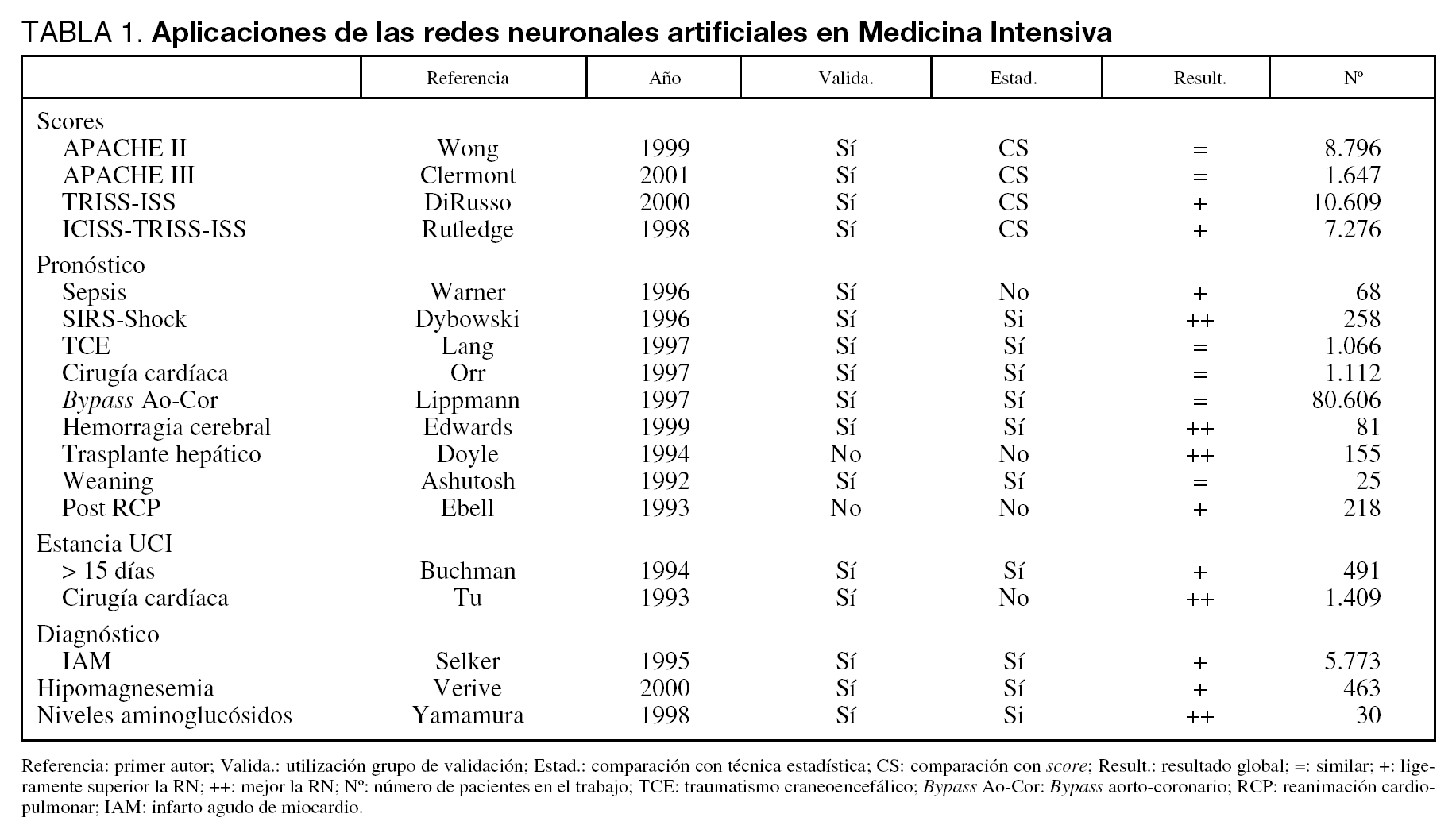
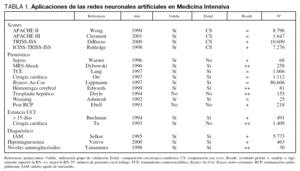
En Medicina Intensiva las RN se han utilizado en diversos problemas. En la tabla 1 mostramos algunos de los trabajos más representativos con sus características fundamentales8-25.
Los objetivos de nuestro trabajo son en primer lugar validar el modelo MPM II en nuestra UCI y compararlo con un modelo construido reajustando los coeficientes correspondientes a las variables de la ecuación logística, y en segundo construir un modelo basado en la metodología de RN con las mismas variables. Los dos modelos (RL y RN) se validan en un grupo independiente de pacientes (cronológicamente posterior). Comparar el modelo MPM II, no sólo con un modelo reajustado, sino con un modelo basado en RN, constituye la contribución de nuestro estudio.
PACIENTES Y MÉTODO
Pacientes
El estudio se ha realizado en la UCI polivalente (médica y quirúrgica) de 10 camas ubicada en el Hospital Universitario Arnau de Vilanova de Lleida. Se informó al Comité Ético del Hospital de la realización del estudio, no se precisó consentimiento informado, ya que todas las variables se recogían para el diagnóstico y el tratamiento de los pacientes y se aseguró en todo momento el anonimato de los mismos.
Se recogieron, de forma prospectiva, los ingresos de enero de 1996 a diciembre de 1999 que formaron el grupo de Desarrollo, y de enero de 2000 hasta diciembre de 2000 que constituyeron el grupo de Validación. Todos los datos demográficos y las variables necesarias para calcular los modelos MPM II-0 (Admisión) y MPM II-24 (24-horas) fueron recogidos por un equipo entrenado2.
Modelo MPM II reajustado según regresión logística
Por las características de nuestra serie (tamaño y porcentaje de mortalidad) aplicamos la estrategia de reajustar los coeficientes de la RL de acuerdo con el método sugerido por Zhu et al3.
Reajustar un modelo de RL supone calcular los nuevos coeficientes de las variables predictoras utilizando los valores propios de cada UCI26.
Diseño de la red neuronal artificial
Para el desarrollo de nuestra aplicación utilizamos una arquitectura de perceptrón multicapa (MLP-multilayered perceptron) entrenado con algoritmo de retropropagación del error (backpropagation). Para introducirse en el tema existen revisiones sencillas en la literatura6,27.
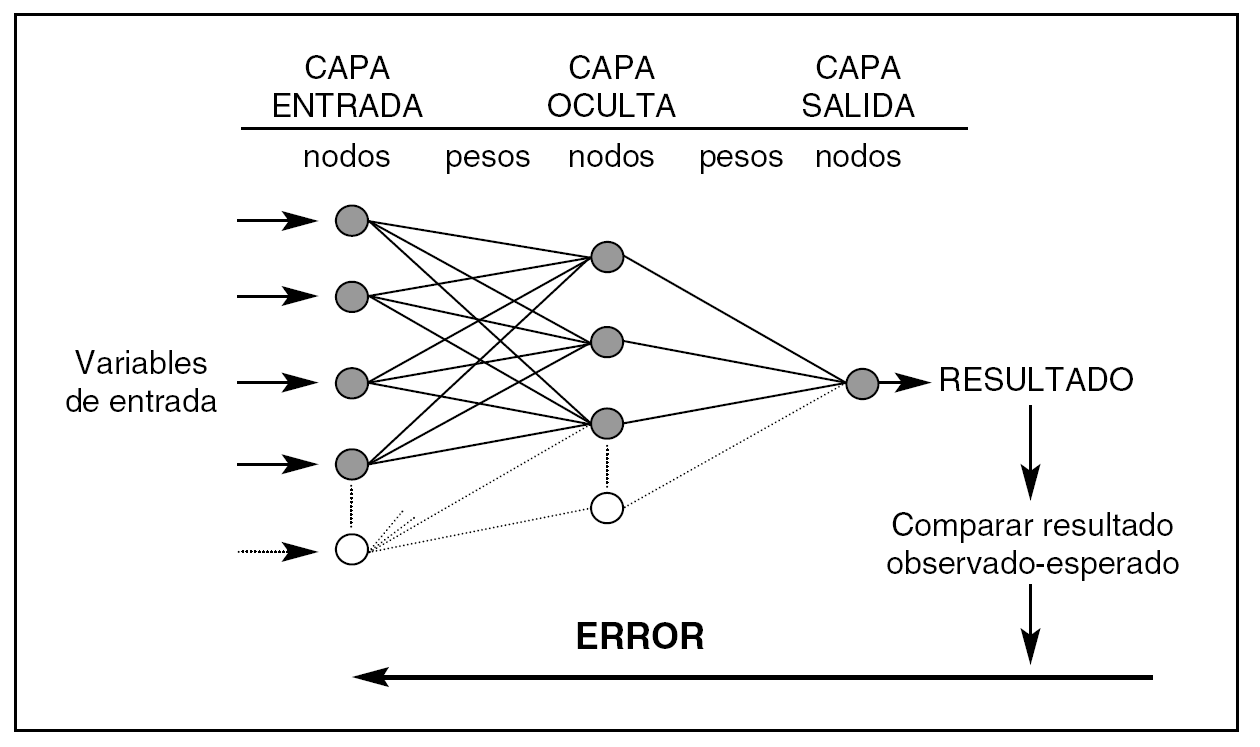
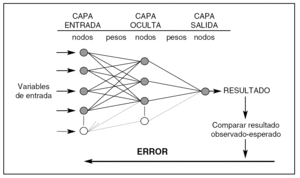
Una RN (fig. 1) consta de capas que están formadas por nodos. La capa de entrada recibe los valores de las variables predictoras, la capa oculta es donde se realizan los procesos de ajuste, y la capa de salida donde se obtienen los resultados de la red (output). Los nodos están unidos por unos parámetros internos (pesos = weights) cuyos valores se modifican de acuerdo a los valores que reciben los nodos y según la función de red que se les aplica. La complejidad de una RN depende de la cantidad de parámetros internos que contenga.
Figura 1. Arquitectura de una red neuronal artificial (perceptrón de tres capas). Los pesos son los parámetros que deben ajustarse durante el proceso de entrenamiento para conseguir que la capa de salida de resultados coincida con los observados. El error entre lo observado y el resultado de la red se propaga hacia atrás (backpropagation) y debe ir disminuyendo en las sucesivas iteraciones en las que se presentan los valores de las variables predictoras. La complejidad de una red depende del número de nodos de su capa oculta.
La RN precisa de un proceso de entrenamiento para alcanzar la capacidad de generalización, primero comenzamos con valores aleatorios de los pesos que deben de modificarse de forma iterativa (cada vez que presentamos los datos de entrada a la red) para conseguir los resultados más próximos a los valores observados. La finalidad es minimizar el error que se observa de esta diferencia entre los valores de la red y los observados.
La estrategia que se sigue para evitar que la red sobreaprenda (sólo memoriza, pero no tiene capacidad de generalización) es dividir el grupo de Desarrollo en un subgrupo de Entrenamiento (70% del grupo de desarrollo) y un subgrupo de Verificación (30% restante). El subgrupo de Verificación no se emplea en el ajuste de los parámetros, pero la red debe mantener buenos resultados en este subgrupo, durante el entrenamiento, para asegurar que la red adquiere la capacidad de generalización.
La arquitectura óptima de la red (número de capas ocultas y de nodos que las forman) se alcanza con un método empírico observando la evolución del error en el subgrupo de Verificación28. El valor de salida de nuestra red es la probabilidad de muerte y se interpreta con un valor de 0 a 1. Para la creación de la RN utilizamos el programa comercial Qnet 97 (Vesta Services Inc.). Los parámetros de entrenamiento modificables en el software (momento, coeficiente de aprendizaje, etc.) fueron optimizados para alcanzar el mejor resultado de la red.
Comparación de los modelos
Para comparar los distintos modelos medimos su capacidad de discriminación y calibración; la discriminación calculando el porcentaje de pacientes correctamente clasificados (PCC) con el punto de corte a 0,5 y con el área bajo la curva ROC (ABC)29,30; y la calibración usando el test de Hosmer-Lemeshow C31, construyendo la curva de calibración y calculando las razones de mortalidad estandarizada (RME)32. Estos cálculos se realizan tanto en el grupo de Desarrollo como en el de Validación. Utilizamos el test de Bland-Altman para analizar las probabilidades generadas por cada modelo33 y el coeficiente de correlación intraclase (CCI) para valorar la concordancia entre los mismos34. El análisis estadístico se realizó con el programa SPSS (versión 11.0).
RESULTADOS
Características del grupo de estudio
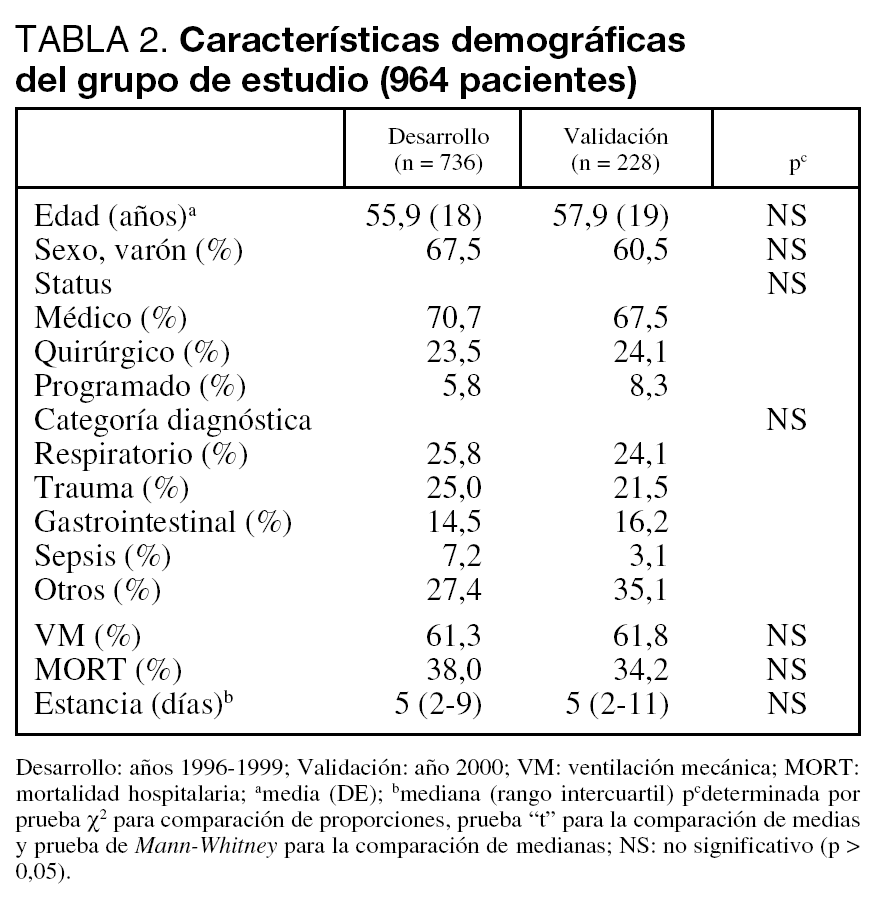
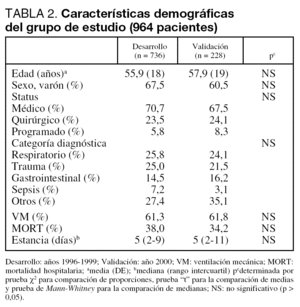
Se analizan un total de 964 pacientes divididos en el grupo de Desarrollo (736) y el de Validación (228).
Nuestra población se define por tener pocos pacientes programados (quirúrgicos), que nos conduce a una mortalidad hospitalaria alta y un incremento en la estancia media en UCI. No encontramos diferencias significativas en los distintos subgrupos definidos en el estudio (tabla 2). Tampoco apreciamos diferencias significativas al analizar las características demográficas en los distintos años que abarcaba el estudio.
Modelo MPM II reajustado según regresión logística
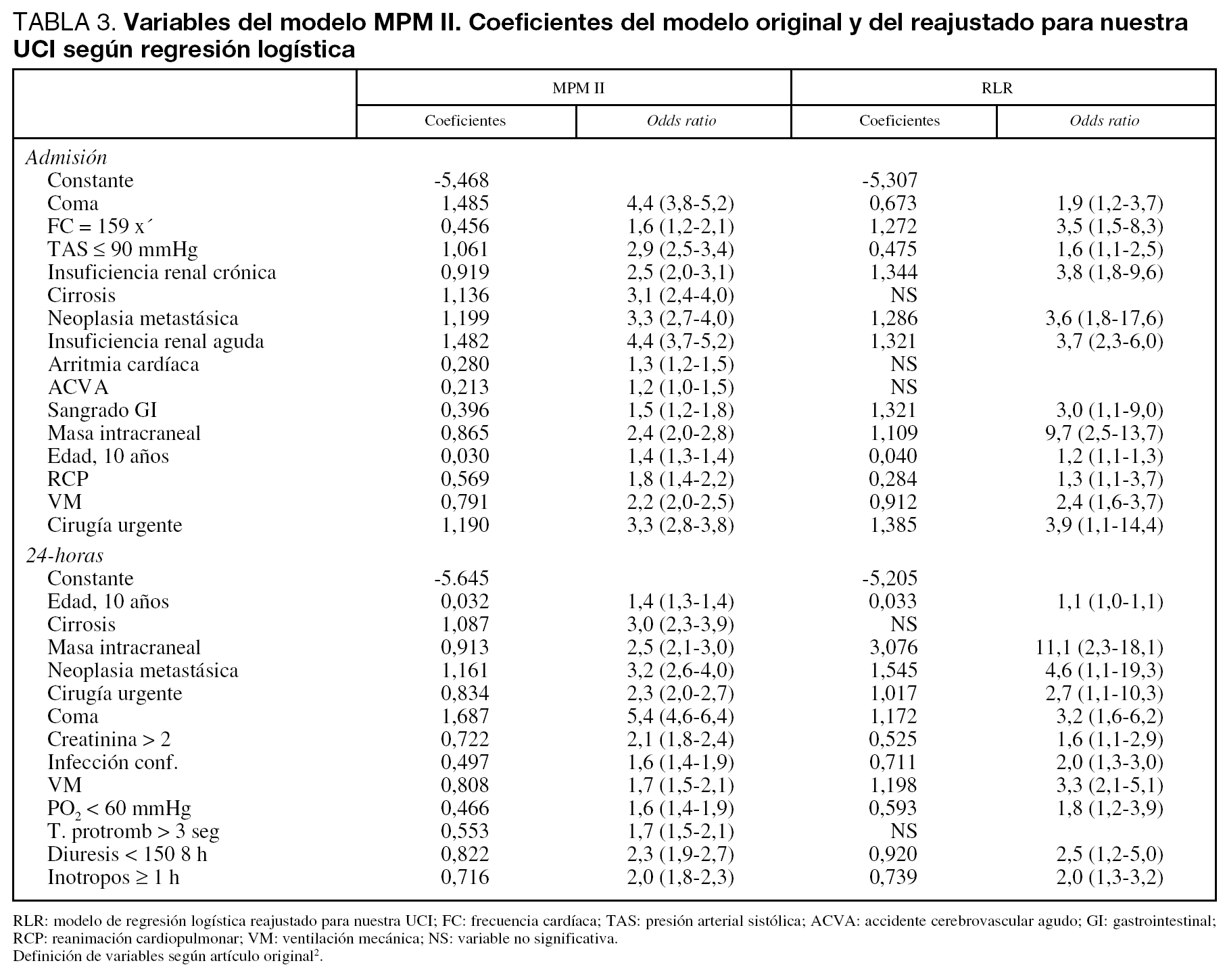
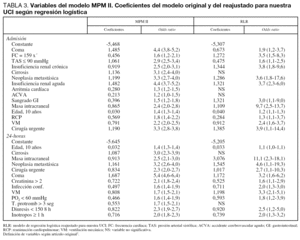
Al reajustar los coeficientes del MPM II se obtienen nuevos modelos: el reajustado en el modelo de Admisión (reajuste de regresión logística 0) (RLR-0) y en el modelo de 24-horas (reajuste de regresión logística 24) (RLR-24).
En el modelo Admisión, las variables que no alcanzaron significación estadística fueron: cirrosis, arritmia cardíaca y enfermedad cerebrovascular; en el modelo 24-horas: cirrosis y tiempo de protrombina mayor de 3 segundos sobre el estándar (tabla 3).
Justificamos las diferencias encontradas en los coeficientes por nuestro diferente case-mix, al tener pocos pacientes con cirrosis (sólo 7 pacientes), enfermedad cerebrovascular (33 pacientes) y no incluir a los pacientes coronarios.
Arquitectura de la red neuronal artificial
Las arquitecturas óptimas fueron diferentes para el modelo Admisión (con 4 nodos en la capa oculta) que para el modelo 24-horas (8 nodos). Con redes más complejas (con más nodos en la capa oculta) no mejorábamos la precisión.
Comparación de los modelos
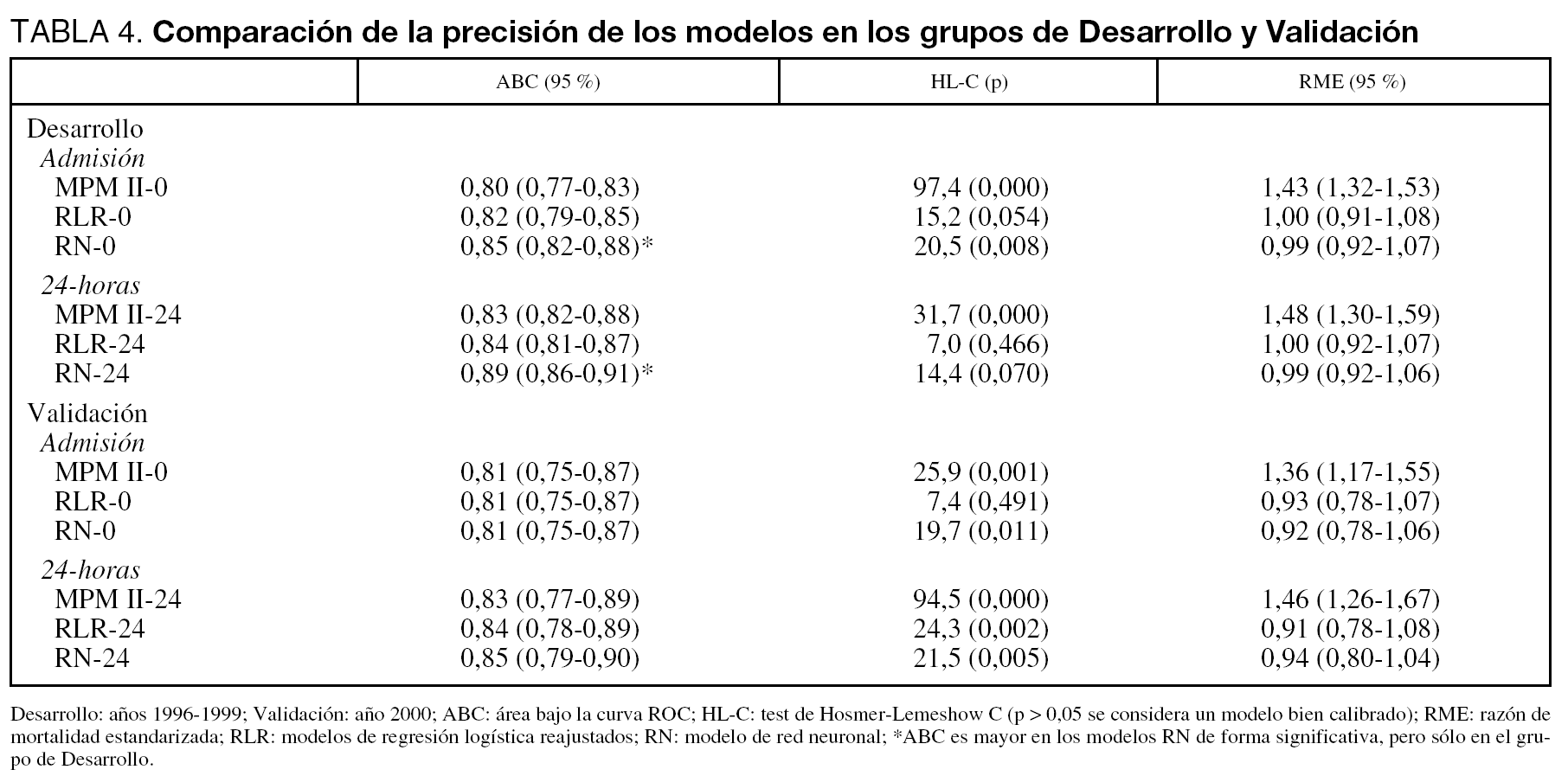
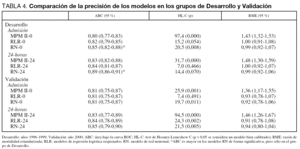
En el grupo de Desarrollo, el modelo MPM II tanto en Admisión como a las 24-horas obtuvo una buena discriminación (ABC de 0,8), pero pobre calibración. Como era esperable, los modelos reajustados (RLR) mejoraron en calibración. Las RN consiguen una mejor discriminación y calibración. En el grupo de Validación se observa similar comportamiento con el modelo MPM II, mejoría en la calibración con los modelos reajustados así como con las redes (tabla 4).
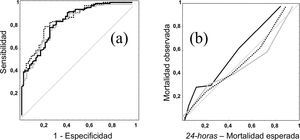
En la figura 2 se muestran las curvas ROC y de calibración del modelo 24-horas en el grupo de Validación (en el modelo Admisión los resultados son similares). Al igual que en las curvas ROC, cuando evaluamos el PCC de los distintos modelos encontramos pocas diferencias, siendo del 74 % en el modelo MPM II-24, 75 % en RLR-24 y del 77 % en el RN-24 (siendo la diferencia máxima entre los modelos de 4 pacientes correctamente clasificados).
Figura 2. Curvas ROC (a) y curvas de calibración (b) del modelo 24-horas. Línea negra modelo MPM II, línea gris modelo de Regresión logística reajustado, y línea de puntos modelo de red neuronal.
En la figura correspondiente a las curvas de calibración observamos la tendencia del modelo MPM II-24 a infraestimar la probabilidad de mortalidad hospitalaria (curva sobre la línea de perfecta calibración).
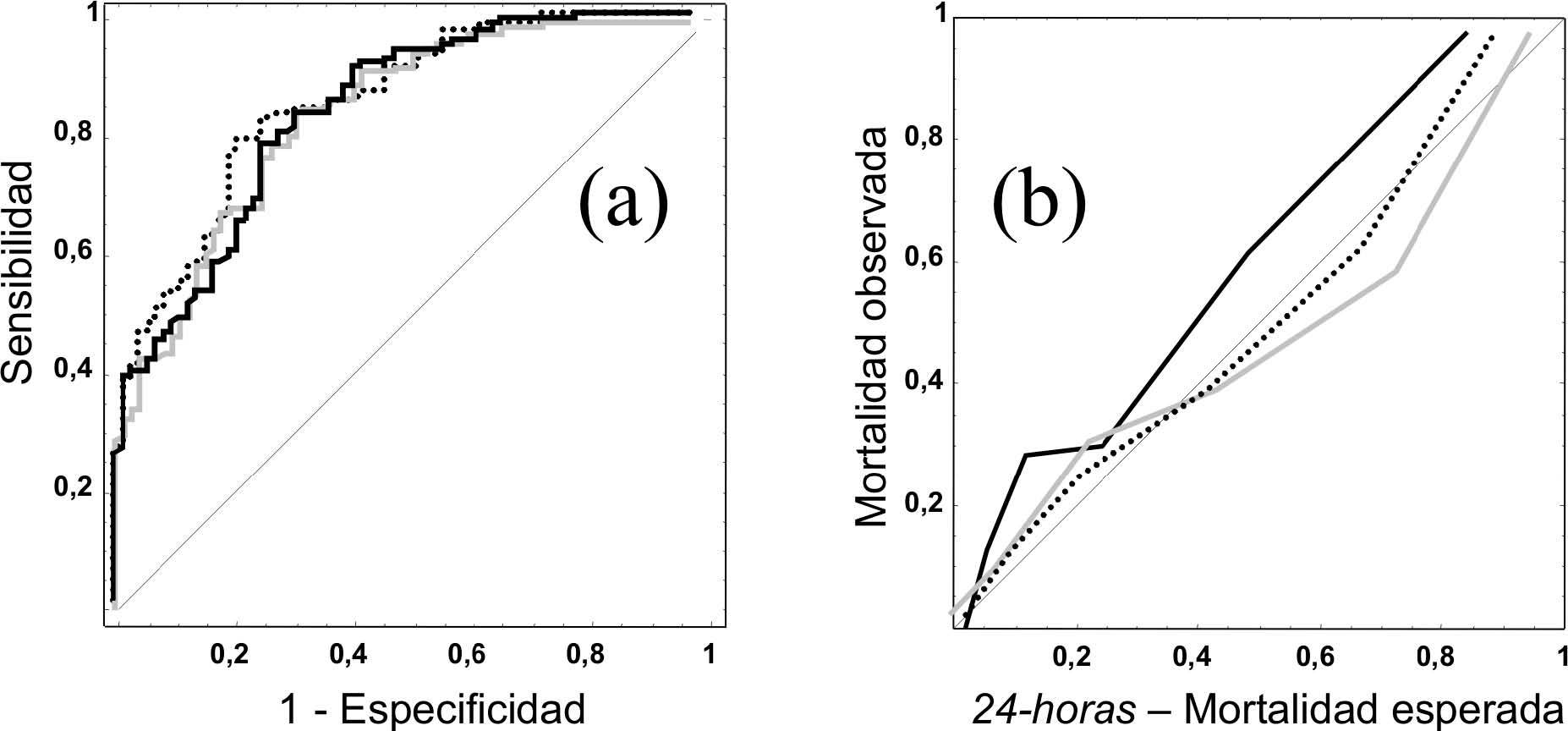
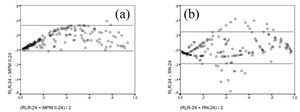
En el modelo 24-horas, la comparación de las probabilidades calculadas por los modelos mostraban algunas diferencias. Si comparamos el RLR-24 y el MPM-24 (fig. 3a) se observa el efecto conseguido con el reajuste del modelo que consigue una mejor calibración y que muestra un CCI de 0,86 (buena concordancia). La comparación entre el RLR-24 y la RN-24 (fig. 3b) nos da un resultado que no sigue un patrón uniforme, con un CCI que en este caso baja a 0,74. Los valores de probabilidad de muerte de algunos pacientes son muy diferentes según el modelo utilizado, lo que indicaba la diferente contribución de las variables predictoras según el modelo considerado.
Figura 3. Gráficos de Bland-Altman de los modelos de predicción de mortalidad a las 24-horas en el grupo de Validación. RLR-24: modelo de regresión logística reajustado. RN-24: modelo de red neuronal. Las líneas horizontales corresponden a ± 2 desviaciones estándar. (a): RLR-24 comparado con MPM II-24. (b): RLR-24 comparado con RN-24.
Como ejemplo para explicar diferencias entre los modelos hicimos un estudio de los casos extremos (un total de 136 pacientes), con diferencias de mortalidad superiores en un 20 %, que nos demostró que en algunos casos (en 70 pacientes) pequeñas variaciones en la variable "edad" (no discriminadas por el modelo MPM II) modificaban la probabilidad esperada según la RN, aunque se mantuvieran los mismos valores en el resto de variables predictoras.
Para evaluar la consistencia de nuestros resultados comprobamos que la utilización de 50 redes entrenadas con distinto grupo de Verificación, asignado al azar, conseguían resultados similares a los expuestos.
DISCUSIÓN
La aplicación de un modelo de predicción de mortalidad puede hacerse con confianza cuando ha sido validado en la población donde se aplica. Las características de nuestra UCI, por su tamaño, bajo número de ingresos programados, alta mortalidad y case-mix, nos apartan de las condiciones medias de la población que sirvió para confeccionar el modelo MPM II. Cuando aplicamos este sistema a nuestra UCI, descubrimos una falta de calibración al obtener una mortalidad superior a la esperada según el modelo. Esta discrepancia nos obliga a evaluar nuestro nivel asistencial y encontrar el modo de obtener un método preciso para estratificar la gravedad de nuestros pacientes que nos sirva como herramienta y control de calidad5. Para conseguir reajustar el modelo podemos utilizar la metodología estadística basada en RL o utilizar una RN.
Las RN han sido utilizadas de forma creciente en Medicina, existiendo múltiples revisiones publicadas. Las aplicaciones más frecuentes se sitúan en el diagnóstico clínico, farmacología y predicción de resultados35-37.
Nuestros resultados no encuentran diferencias significativas entre el modelo reajustado por RL y el conseguido con RN, aunque apreciamos una tendencia de mejores parámetros de discriminación y calibración con las RN. En diversos artículos con hallazgos similares los autores concluyen que la relación existente entre las variables predictoras es independiente y prácticamente lineal38. Nosotros aportamos la visión de que, aunque de forma global los resultados son similares, encontramos pacientes que tienen diferente asignación de probabilidad según el modelo RL o RN. El análisis de este tipo de pacientes descubre que algunas variables (en nuestro caso la edad) contribuyen de forma diferente para ambos modelos. Así, queda planteada la pregunta de cuál de los dos modelos (RL o RN) es más preciso al utilizarlo en nuestra UCI.
En general, una RN es más precisa cuando se cumplen diversas condiciones: la variable final viene expresada como función compleja de las variables predictoras o cuando existen influencias entre las variables predictoras difíciles de encontrar. Por otra parte, las RN son más complicadas, y sus coeficientes no tienen una interpretación fácil de expresar con el lenguaje habitual39.
En nuestros resultados (sobre todo en el modelo 24-horas) la metodología basada en RN apunta mejores resultados, ya que es capaz de encontrar relaciones y efectos no lineales entre las variables del MPM II y la probabilidad de muerte.
En la revisión de Sargent, que analiza 28 trabajos sobre predicción de resultados con RN (comparada con RL), encuentra que las RN son equivalentes o superiores cuando se analizan series con suficiente número de pacientes, aunque también advierte que debe valorarse el sesgo de publicación (tienden a publicarse los trabajos cuando las RN son por lo menos similares o mejores)40.
Las variables empleadas en el modelo MPM II han sido seleccionadas bajo técnicas de RL, lo que también penaliza al modelo RN. Si la selección se hubiera hecho con RN, las variables podrían haber sido otras.
Las limitaciones de nuestro trabajo se basan en dos aspectos. Primero, hemos utilizado un tipo de RN concreto (el perceptrón multicapa con algoritmo de retropropagación del error), utilizar otro tipo de red podría conseguir unos mejores resultados15; además, el empirismo para obtener la arquitectura óptima siempre debe tenerse en cuenta. Y segundo, nuestra serie es pequeña (debido a las características de nuestra UCI y hospital), lo que limita las conclusiones generales del trabajo. Trabajar con un rango de 5 años también introduce factores de confusión que deben tenerse en cuenta. Otra limitación importante es el aspecto de computación de los datos, ya que para el cálculo de la precisión de las redes debemos hacer procedimientos basados en remuestreo intensivo que no hemos mostrado en el artículo para garantizar una mayor claridad en su lectura.
Nuestros resultados son similares a los publicados comparando el modelo APACHE II y APACHE III con las RN8,9.
En conclusión, nuestro trabajo pretende afirmar la necesidad de validar los instrumentos de predicción en cada UCI y la necesidad posterior de reajustar los modelos (al encontrar una falta de calibración) que puede hacerse con técnicas basadas en RL o RN. Poder acercar, de forma sencilla, la metodología basada en redes también puede considerarse una aportación.
Idealmente, la búsqueda de modelos más precisos debe basarse en que estos sean capaces de mantener su precisión cuando se apliquen en poblaciones concretas. Las técnicas de RN pueden ayudarnos en este objetivo.