To determine if potential predictors for invasive mechanical ventilation (IMV) are also determinants for mortality in COVID-19-associated acute respiratory distress syndrome (C-ARDS).
DesignSingle center highly detailed longitudinal observational study.
SettingTertiary hospital ICU: two first COVID-19 pandemic waves, Madrid, Spain.
Patients or participants: 280 patients with C-ARDS, not requiring IMV on admission.
InterventionsNone.
Main variables of interest: Target: endotracheal intubation and IMV, mortality.
Predictors: demographics, hourly evolution of oxygenation, clinical data, and laboratory results.
ResultsThe time between symptom onset and ICU admission, the APACHE II score, the ROX index, and procalcitonin levels in blood were potential predictors related to both IMV and mortality. The ROX index was the most significant predictor associated with IMV, while APACHE II, LDH, and DaysSympICU were the most with mortality.
ConclusionsAccording to the results of the analysis, there are significant predictors linked with IMV and mortality in C-ARDS patients, including the time between symptom onset and ICU admission, the severity of the COVID-19 waves, and several clinical and laboratory measures. These findings may help clinicians to better identify patients at risk for IMV and mortality and improve their management.
Determinar si las variables clínicas independientes que condicionan el inicio de ventilación mecánica invasiva (VMI) son los mismos que condicionan la mortalidad en el síndrome de distrés respiratorio agudo asociado con COVID-19 (C-SDRA).
DiseñoEstudio observacional longitudinal en un solo centro.
ÁmbitoUCI, hospital terciario: primeras dos olas de COVID-19 en Madrid, España.
Pacientes o participantes280 pacientes con C-SDRA que no requieren VMI al ingreso en UCI.
IntervencionesNinguna.
Principales variables de interésObjetivo: VMI y Mortalidad.
Predictores: demográficos, variables clínicas, resultados de laboratorio y evolución de la oxigenación.
ResultadosEl tiempo entre el inicio de los síntomas y el ingreso en la UCI, la puntuación APACHE II, el índice ROX y los niveles de procalcitonina en sangre eran posibles predictores relacionados tanto con la IMV como con la mortalidad. El índice ROX fue el predictor más significativo asociada con la IMV, mientras que APACHE II, LDH y DaysSympICU fueron los más influyentes en la mortalidad.
ConclusionesSegún los resultados obtenidos se identifican predictores significativos vinculados con la VMI y mortalidad en pacientes con C-ARDS, incluido el tiempo entre el inicio de los síntomas y el ingreso en la UCI, la gravedad de las olas de COVID-19 y varias medidas clínicas y de laboratorio. Estos hallazgos pueden ayudar a los médicos a identificar mejor a los pacientes en riesgo de IMV y mortalidad y mejorar su manejo.
Invasive mechanical ventilation (IMV) is a cornerstone of organ support in severe COVID-19 patients with acute respiratory distress syndrome (ARDS). As widely experienced in ICUs during the SARS-CoV-2 pandemic, IMV frequently causes complications.1,2 Hospital services were overwhelmed not only by the surge of patients, but also by scarce human resources and equipment, lack of sufficient mechanical ventilators being probably the most relevant. In surge scenarios, appropriate triage strategies are therefore needed to allocate IMV or alternatives such as high flow nasal prongs. These strategies should be based on the knowledge and understanding of specific potential predictors3 that could help clinicians to personalize decisions regarding IMV.
There is still considerable controversy regarding who and when to intubate. Several recent studies have addressed the subject,4 although bias cannot be excluded in observational non-randomized trials. A retrospective study suggested that early intubation and IMV is associated with favorable outcomes but included only intubated patients instead of the whole population at risk.
Previous studies have identified covid-19 progression predictors including age, comorbidities, renal function, or immunodeficiency5 using traditional statistical approaches, where collinearity of data cannot be ruled out. Artificial intelligence (AI) is currently being used for COVID-19 risk stratification,6 studying multiple clinical features to increase effectiveness and efficiency in diagnosis, treatment, and prognosis. Self-explainable Machine learning (ML) techniques can help with risk factor selection through ranking methodologies.7 In this context, the utilization of artificial intelligence (AI) holds potential in facilitating the development of a conceptual model aimed at comparing the significance of variables. This can be achieved by employing regularization models8 to enhance predictor selection, followed by the implementation of the Generalized Linear Mixed-effects Model (GLMM)9–11 to construct the said conceptual model. Such an approach becomes particularly relevant when assessing and comparing outcomes across different AI models, enabling a comprehensive evaluation of variable significance. This is a novel methodology, leveraging modern machine learning techniques to provide rigorous and applicable insight into relevant clinical questions when randomized clinical trials are not feasible. From here on, in this paper, we aim to determine if potential predictors for invasive mechanical ventilation (IMV) are also determinants for mortality in COVID-19-associated acute respiratory distress syndrome (C-ARDS) while comparing the significance of variables in both cases.
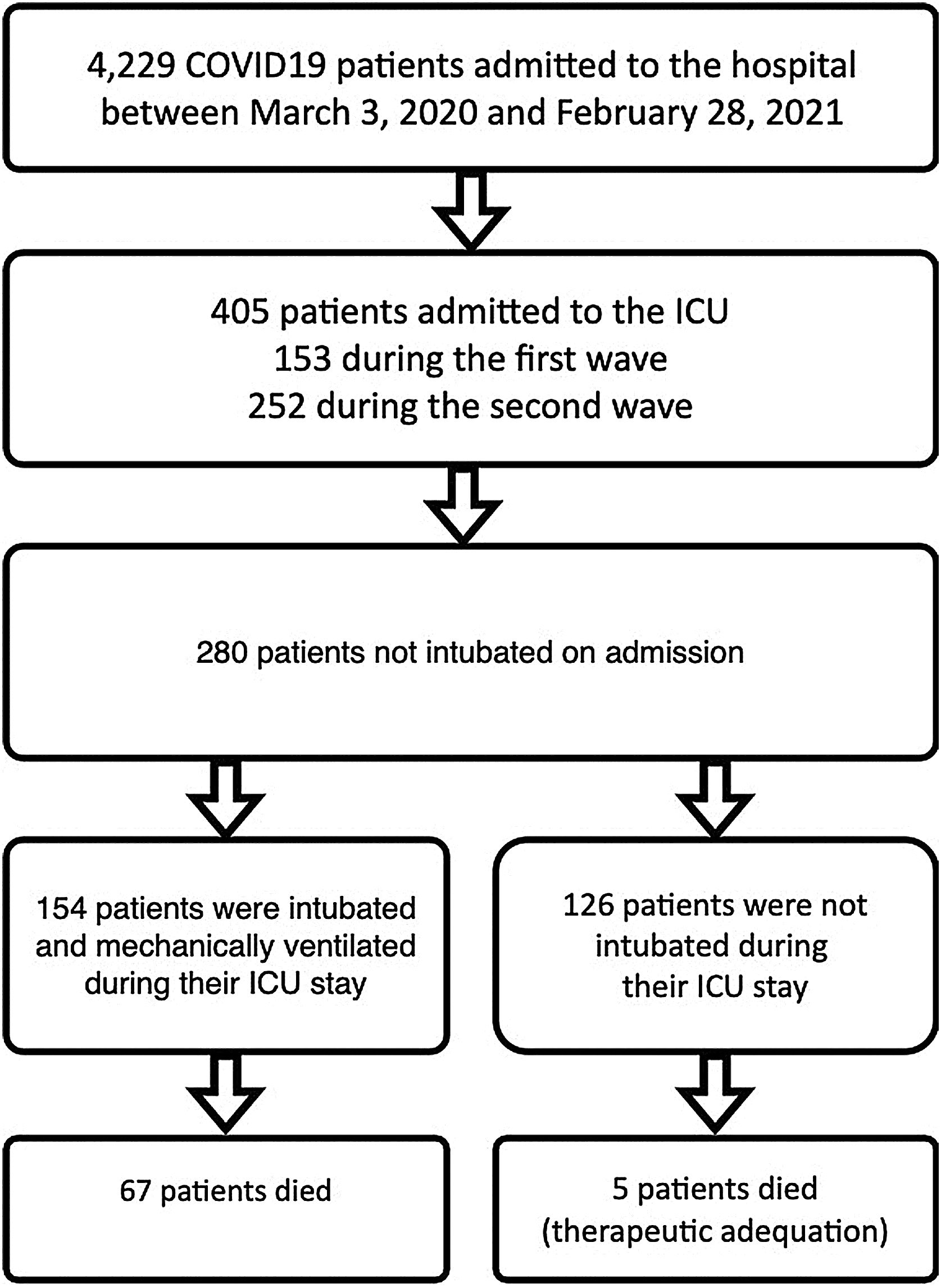
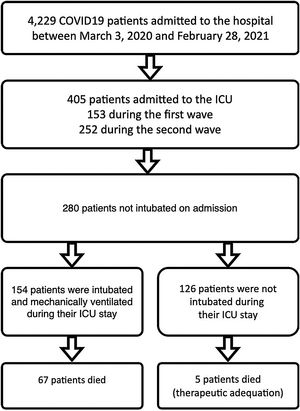
Patients and methodsSelection and description of patientsIn our retrospective observational study, we have collected and curated data from our electronic medical records (EMR) from March 3rd of 2020 through February 28th of 2021. We selected patients admitted to our ICU at San Carlos Hospital (HCSC) in Madrid (Fig. 1) but were initially not mechanically ventilated. The selection of patients considered just COVID-19 pneumonia patients, incidental COVID-19 was excluded. The age range for inclusion was restricted to individuals aged 18 years or older.
COVID-19 patients admitted during first and second pandemic waves. The cohort comprises 280 severe COVID-19 patients admitted to the ICU Department at HCSC in Madrid, Spain, between March 3, 2020, and February 28, 2021. During this time period, SARS-COV-2 wild-type and subsequently alpha variants were prevalent in Spain. Over the study time period 4229 covid-19 patients were admitted to HCSC, 405 of whom required ICU admission (first wave: 153, second wave: 252 patients).
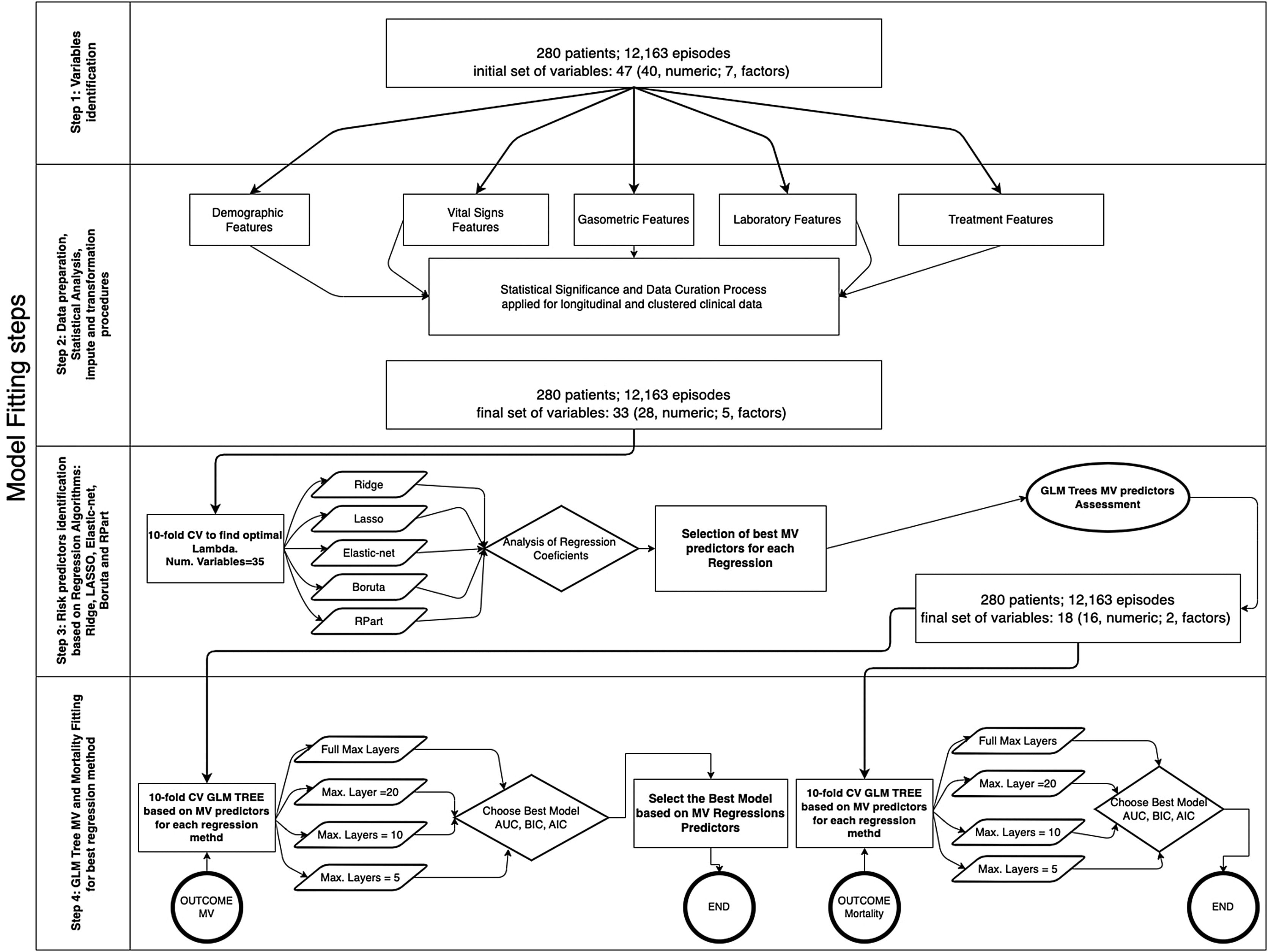
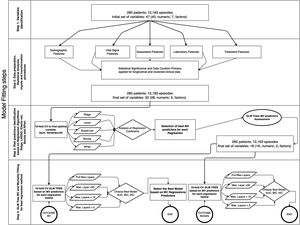
The database comprises hourly data points for each patient during the first five days. Afterwards, we utilized multi-stage machine learning algorithms to assess the most significant variables in predicting invasive mechanical ventilation (IMV) and ICU mortality (Fig. 2). It is worth noting that 28-day mortality, while frequently used in large studies like RECOVERY, may not be a suitable outcome measure in COVID-19 patients due to the possibility of delayed mortality.
Methodology for fitting the machine learning algorithms. In a previous stage, Figure 5 in Supplementary material shows the complete workflow, from the cohort selection according to clinical needs to the implementation of the algorithms that have been included in the explanation. The first step involves the cohort selection as well as the initial group of variables considered in this study, The second step consists in the implementation of a statistical study of each variable. This step also involves correlation (Figure 6 in Supplementary material) imputation and transformations procedures in order to dispose of the most accurate data in the following steps. The third step analyzed the most significant predictors based on five Machine Learning (ML) techniques linked with regression analysis based on 10-fold cross-validation regressions. The fourth and last step identifies the behavior of each predictor attending to different proposes. The first one is related to mechanical ventilation needs attending to different settings in the Generalized Linear Mixed Model (GLMM) Tree (depth of layers) looking for the best balance between performance (Akaike Information Criterion (AIC), Bayesian information criterion (BIC), Area Under the Roc Curve (ROC) and more parameters within the table III) and explainability of the model. The second one is related to the most representative mortality predictors but following the same balance objective.
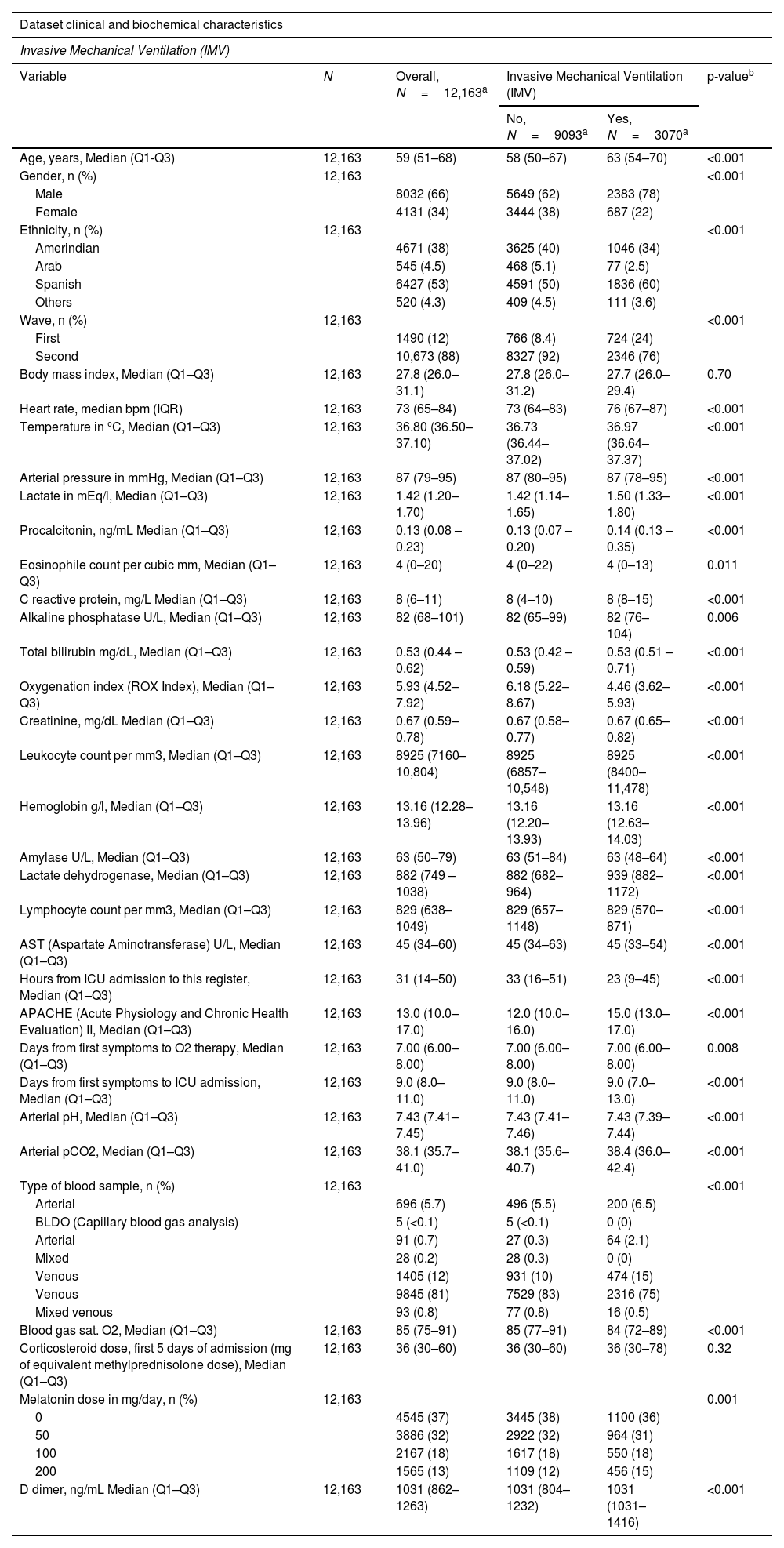
All data were registered in our electronic medical record (ICCA Philips). A total of 12,163 longitudinal sets of hourly clinical and lab data were gathered. Longitudinal sets are grouped in clustered events associated with patients. Each entry contains demographics data, first or second wave admission, time elapsed from start of symptoms to O2 therapy and ICU admission, APACHE II score, monitoring, blood gases and therapy-related data. We discarded variables with more than 33% of missing values for consistency. We used mode imputation or mean imputation to complete missing values of the remaining variables. Tables 1 and 2 show the predictors that were finally used for the purposes of the study.
Group of predictors for Invasive Mechanical Ventilation regression purposes.
| Dataset clinical and biochemical characteristics | |||||
|---|---|---|---|---|---|
| Invasive Mechanical Ventilation (IMV) | |||||
| Variable | N | Overall, N=12,163a | Invasive Mechanical Ventilation (IMV) | p-valueb | |
| No, N=9093a | Yes, N=3070a | ||||
| Age, years, Median (Q1-Q3) | 12,163 | 59 (51–68) | 58 (50–67) | 63 (54–70) | <0.001 |
| Gender, n (%) | 12,163 | <0.001 | |||
| Male | 8032 (66) | 5649 (62) | 2383 (78) | ||
| Female | 4131 (34) | 3444 (38) | 687 (22) | ||
| Ethnicity, n (%) | 12,163 | <0.001 | |||
| Amerindian | 4671 (38) | 3625 (40) | 1046 (34) | ||
| Arab | 545 (4.5) | 468 (5.1) | 77 (2.5) | ||
| Spanish | 6427 (53) | 4591 (50) | 1836 (60) | ||
| Others | 520 (4.3) | 409 (4.5) | 111 (3.6) | ||
| Wave, n (%) | 12,163 | <0.001 | |||
| First | 1490 (12) | 766 (8.4) | 724 (24) | ||
| Second | 10,673 (88) | 8327 (92) | 2346 (76) | ||
| Body mass index, Median (Q1–Q3) | 12,163 | 27.8 (26.0–31.1) | 27.8 (26.0–31.2) | 27.7 (26.0–29.4) | 0.70 |
| Heart rate, median bpm (IQR) | 12,163 | 73 (65–84) | 73 (64–83) | 76 (67–87) | <0.001 |
| Temperature in ºC, Median (Q1–Q3) | 12,163 | 36.80 (36.50–37.10) | 36.73 (36.44–37.02) | 36.97 (36.64–37.37) | <0.001 |
| Arterial pressure in mmHg, Median (Q1–Q3) | 12,163 | 87 (79–95) | 87 (80–95) | 87 (78–95) | <0.001 |
| Lactate in mEq/l, Median (Q1–Q3) | 12,163 | 1.42 (1.20–1.70) | 1.42 (1.14–1.65) | 1.50 (1.33–1.80) | <0.001 |
| Procalcitonin, ng/mL Median (Q1–Q3) | 12,163 | 0.13 (0.08 – 0.23) | 0.13 (0.07 – 0.20) | 0.14 (0.13 – 0.35) | <0.001 |
| Eosinophile count per cubic mm, Median (Q1–Q3) | 12,163 | 4 (0–20) | 4 (0–22) | 4 (0–13) | 0.011 |
| C reactive protein, mg/L Median (Q1–Q3) | 12,163 | 8 (6–11) | 8 (4–10) | 8 (8–15) | <0.001 |
| Alkaline phosphatase U/L, Median (Q1–Q3) | 12,163 | 82 (68–101) | 82 (65–99) | 82 (76–104) | 0.006 |
| Total bilirubin mg/dL, Median (Q1–Q3) | 12,163 | 0.53 (0.44 – 0.62) | 0.53 (0.42 – 0.59) | 0.53 (0.51 – 0.71) | <0.001 |
| Oxygenation index (ROX Index), Median (Q1–Q3) | 12,163 | 5.93 (4.52–7.92) | 6.18 (5.22–8.67) | 4.46 (3.62–5.93) | <0.001 |
| Creatinine, mg/dL Median (Q1–Q3) | 12,163 | 0.67 (0.59–0.78) | 0.67 (0.58–0.77) | 0.67 (0.65–0.82) | <0.001 |
| Leukocyte count per mm3, Median (Q1–Q3) | 12,163 | 8925 (7160–10,804) | 8925 (6857–10,548) | 8925 (8400–11,478) | <0.001 |
| Hemoglobin g/l, Median (Q1–Q3) | 12,163 | 13.16 (12.28–13.96) | 13.16 (12.20–13.93) | 13.16 (12.63–14.03) | <0.001 |
| Amylase U/L, Median (Q1–Q3) | 12,163 | 63 (50–79) | 63 (51–84) | 63 (48–64) | <0.001 |
| Lactate dehydrogenase, Median (Q1–Q3) | 12,163 | 882 (749 – 1038) | 882 (682–964) | 939 (882–1172) | <0.001 |
| Lymphocyte count per mm3, Median (Q1–Q3) | 12,163 | 829 (638–1049) | 829 (657–1148) | 829 (570–871) | <0.001 |
| AST (Aspartate Aminotransferase) U/L, Median (Q1–Q3) | 12,163 | 45 (34–60) | 45 (34–63) | 45 (33–54) | <0.001 |
| Hours from ICU admission to this register, Median (Q1–Q3) | 12,163 | 31 (14–50) | 33 (16–51) | 23 (9–45) | <0.001 |
| APACHE (Acute Physiology and Chronic Health Evaluation) II, Median (Q1–Q3) | 12,163 | 13.0 (10.0–17.0) | 12.0 (10.0–16.0) | 15.0 (13.0–17.0) | <0.001 |
| Days from first symptoms to O2 therapy, Median (Q1–Q3) | 12,163 | 7.00 (6.00–8.00) | 7.00 (6.00–8.00) | 7.00 (6.00–8.00) | 0.008 |
| Days from first symptoms to ICU admission, Median (Q1–Q3) | 12,163 | 9.0 (8.0–11.0) | 9.0 (8.0–11.0) | 9.0 (7.0–13.0) | <0.001 |
| Arterial pH, Median (Q1–Q3) | 12,163 | 7.43 (7.41–7.45) | 7.43 (7.41–7.46) | 7.43 (7.39–7.44) | <0.001 |
| Arterial pCO2, Median (Q1–Q3) | 12,163 | 38.1 (35.7–41.0) | 38.1 (35.6–40.7) | 38.4 (36.0–42.4) | <0.001 |
| Type of blood sample, n (%) | 12,163 | <0.001 | |||
| Arterial | 696 (5.7) | 496 (5.5) | 200 (6.5) | ||
| BLDO (Capillary blood gas analysis) | 5 (<0.1) | 5 (<0.1) | 0 (0) | ||
| Arterial | 91 (0.7) | 27 (0.3) | 64 (2.1) | ||
| Mixed | 28 (0.2) | 28 (0.3) | 0 (0) | ||
| Venous | 1405 (12) | 931 (10) | 474 (15) | ||
| Venous | 9845 (81) | 7529 (83) | 2316 (75) | ||
| Mixed venous | 93 (0.8) | 77 (0.8) | 16 (0.5) | ||
| Blood gas sat. O2, Median (Q1–Q3) | 12,163 | 85 (75–91) | 85 (77–91) | 84 (72–89) | <0.001 |
| Corticosteroid dose, first 5 days of admission (mg of equivalent methylprednisolone dose), Median (Q1–Q3) | 12,163 | 36 (30–60) | 36 (30–60) | 36 (30–78) | 0.32 |
| Melatonin dose in mg/day, n (%) | 12,163 | 0.001 | |||
| 0 | 4545 (37) | 3445 (38) | 1100 (36) | ||
| 50 | 3886 (32) | 2922 (32) | 964 (31) | ||
| 100 | 2167 (18) | 1617 (18) | 550 (18) | ||
| 200 | 1565 (13) | 1109 (12) | 456 (15) | ||
| D dimer, ng/mL Median (Q1–Q3) | 12,163 | 1031 (862–1263) | 1031 (804–1232) | 1031 (1031–1416) | <0.001 |
This group of predictors will be applied in the selection procedure linked with the five regression algorithms: Ridge, LASSO, Elastic, Boruta and R-part Based on the reached results, the group of predictors are going to be reduced attending to its behavior related to IMV needs. Figures 7–11 (Supplementary material) shows the results from each regression procedure where R-Part was finally selected due to its good balance between model performance and explicability of results.
Data updated June 22, 2023.
IMV Results. Group of predictors used for mortality prediction with GLMM tree algorithm.
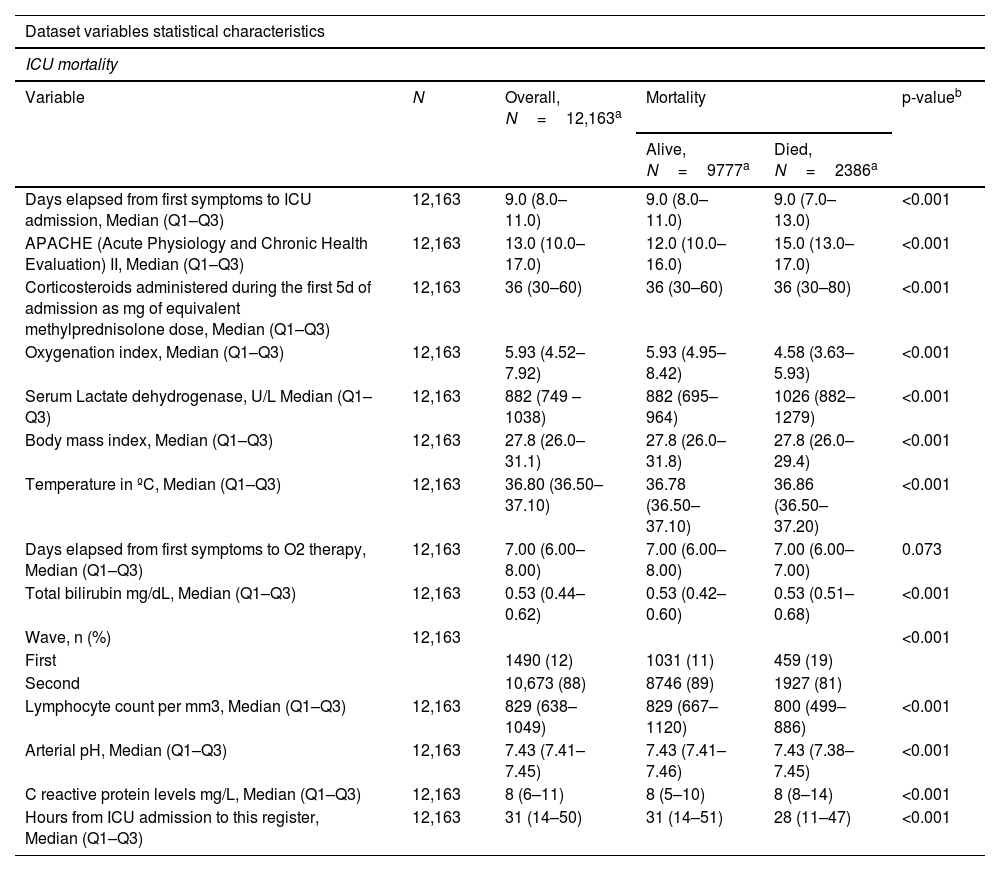
| Dataset variables statistical characteristics | |||||
|---|---|---|---|---|---|
| ICU mortality | |||||
| Variable | N | Overall, N=12,163a | Mortality | p-valueb | |
| Alive, N=9777a | Died, N=2386a | ||||
| Days elapsed from first symptoms to ICU admission, Median (Q1–Q3) | 12,163 | 9.0 (8.0–11.0) | 9.0 (8.0–11.0) | 9.0 (7.0–13.0) | <0.001 |
| APACHE (Acute Physiology and Chronic Health Evaluation) II, Median (Q1–Q3) | 12,163 | 13.0 (10.0–17.0) | 12.0 (10.0–16.0) | 15.0 (13.0–17.0) | <0.001 |
| Corticosteroids administered during the first 5d of admission as mg of equivalent methylprednisolone dose, Median (Q1–Q3) | 12,163 | 36 (30–60) | 36 (30–60) | 36 (30–80) | <0.001 |
| Oxygenation index, Median (Q1–Q3) | 12,163 | 5.93 (4.52–7.92) | 5.93 (4.95–8.42) | 4.58 (3.63–5.93) | <0.001 |
| Serum Lactate dehydrogenase, U/L Median (Q1–Q3) | 12,163 | 882 (749 – 1038) | 882 (695–964) | 1026 (882–1279) | <0.001 |
| Body mass index, Median (Q1–Q3) | 12,163 | 27.8 (26.0–31.1) | 27.8 (26.0–31.8) | 27.8 (26.0–29.4) | <0.001 |
| Temperature in ºC, Median (Q1–Q3) | 12,163 | 36.80 (36.50–37.10) | 36.78 (36.50–37.10) | 36.86 (36.50–37.20) | <0.001 |
| Days elapsed from first symptoms to O2 therapy, Median (Q1–Q3) | 12,163 | 7.00 (6.00–8.00) | 7.00 (6.00–8.00) | 7.00 (6.00–7.00) | 0.073 |
| Total bilirubin mg/dL, Median (Q1–Q3) | 12,163 | 0.53 (0.44–0.62) | 0.53 (0.42–0.60) | 0.53 (0.51–0.68) | <0.001 |
| Wave, n (%) | 12,163 | <0.001 | |||
| First | 1490 (12) | 1031 (11) | 459 (19) | ||
| Second | 10,673 (88) | 8746 (89) | 1927 (81) | ||
| Lymphocyte count per mm3, Median (Q1–Q3) | 12,163 | 829 (638–1049) | 829 (667–1120) | 800 (499–886) | <0.001 |
| Arterial pH, Median (Q1–Q3) | 12,163 | 7.43 (7.41–7.45) | 7.43 (7.41–7.46) | 7.43 (7.38–7.45) | <0.001 |
| C reactive protein levels mg/L, Median (Q1–Q3) | 12,163 | 8 (6–11) | 8 (5–10) | 8 (8–14) | <0.001 |
| Hours from ICU admission to this register, Median (Q1–Q3) | 12,163 | 31 (14–50) | 31 (14–51) | 28 (11–47) | <0.001 |
Data updated June 22, 2023.
Data were anonymized, excluding demographic or temporal information. The study protocol was approved by the local ethics committee (approval code 22/007-E), who waived the need for informed consent due to the retrospective non-interventional nature of the study.
Methods and techniquesData collected as described above were used to fit the model12 following four steps for the whole process, as shown in Fig. 2. Considering that our data involve a concatenation of longitudinal data for each patient in different events, it was necessary to identify correlations within the cluster when trying to build an accurate prediction model.10
The different regression approaches to select potential predictors for IMV and ICU mortality risk tested were: LASSO,13 Ridge,14 Elastic-net,15 Boruta16 and R-Part.17 LASSO, Ridge and Elastic-net perform an automatic predictor selection supported by L1 and L2 regularization terms18 that minimizes the risk of overfitting, reducing variance and reaching an attenuation effect over the correlation between features. Boruta19 is a feature selection model based on a Random Forest algorithm that selects all the risk predictors that are relevant for classification purposes defined as all-relevant problems. R-Part17 builds a classification model based on binary trees. R-Part varImp function20 identifies the effect of model predictors based on the loss function mean squared error. In any case, potential predictors have been analyzed and confirmed or rejected based on clinical criteria.
After identifying the optimal set of potential predictors (Figure 10–14 in Supplementary material), clustering effects by patient and temporal distribution, as well as cutoff points of the significant variables and their interactions were assessed with GLMM Trees.9–11 To build these trees, we took the entire dataset into account, grouping data by patient and data charting time as random variables to fit the model.12 This fitting methodology avoids both over and underfitting effects that could impact the model’s performance.21 Models were implemented based on a 10-fold cross validation strategy using a four-depth-of-layers (full, 5, 10 and 20) strategy. This means the fitting procedure was executed ten times per algorithm implementation. It’s necessary to remark that the positive class for the invasive mechanical ventilation (IMV) variable refers to cases where IMV is required, while the positive class for the ICU mortality variable is related to cases where patients die. It is worth mentioning that the focus of the study is on identifying independent variables and their associated thresholds with IMV and ICU mortality, without defining specific categories to predict.
We used a GLMM Tree to build conceptual models that explain the association between the potential predictors and the two outcome variables. This algorithm accounts for data clusters and temporal characteristics of the dataset, utilizing a mixed-effect strategy to combine the potential predictors that influence the outcome variables. Additionally, the algorithm provides a cut-off value for variables, allowing for comparison with clinical experience.
GLMM Tree performance metrics were Area Under the Curve of Sensibility-Specificity (AUC), the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC),22 as well as the deviance, the likelihood statistical,23 and the sensitivity and specificity parameters. All the regression and GLMM Tree models were fitted with the same subset of variables shown in Table 1.
We used both regressions and GLMM family trees to gain a wider understanding of potential predictors for IMV and ICU mortality. This combined approach offers more intuitive decision-making compared to black-box modeling strategies. We assessed each predictor's effectiveness and used the same set of variables (Table 2) to build an ICU mortality model for the entire cohort. The study's anonymized database and scripts can be found on the associated GitHub repository.24 The database will be published in PhysioNet25 project in order to disseminate and exchange the anonymized clinical records looking for cooperative project replication.
ResultsPatient characteristicsThe complete cohort consisted of 280 patients who were included in the study. A total of 154 patients (55 %) required IMV after ICU admission (Fig. 1), 65 of 80 patients (81.2 %) during the first and 89 of 200 patients (44.5 %) during the second wave. ICU mortality of the whole cohort was 25.7% (72 of 280 patients), 33.7% (27 of 80 patients) during the first and 22.5% (45 of 200 patients) in the second wave. Table 2 shows IMV and ICU mortality predictors for the whole patient’s cohort. Mean registers per patient was 43.4, for a total of 12,163 hourly registers in the whole database (Figure 12 in complementary material).
Significance of predictorsR-Part classification achieves the best and most clinically plausible results in selecting the twelve most representative predictors for IMV and ICU mortality from the whole group of available potential predictors (Table 2). Concerning this subset of predictors, the final selection is based on decreasing order of importance, according to results reached by the loss function (mean squared error), scaled from 0 to 100 points. Taking into account this premise, the predictors are: days from first symptoms to ICU admission (100), the APACHE II score (92.25), the oxygenation index, ROX index (72.46), blood procalcitonin (69.59), serum lactic dehydrogenase (54.45), total serum bilirubin (36.54), the COVID-19 wave (31.18), the dose of corticosteroids administered during the first five days of admission (30.96), lymphocyte count (15.57), pH (13.29), BMI (12.76), C-reactive protein (12.74), time to oxygen therapy (12.42) and body temperature (10.82).
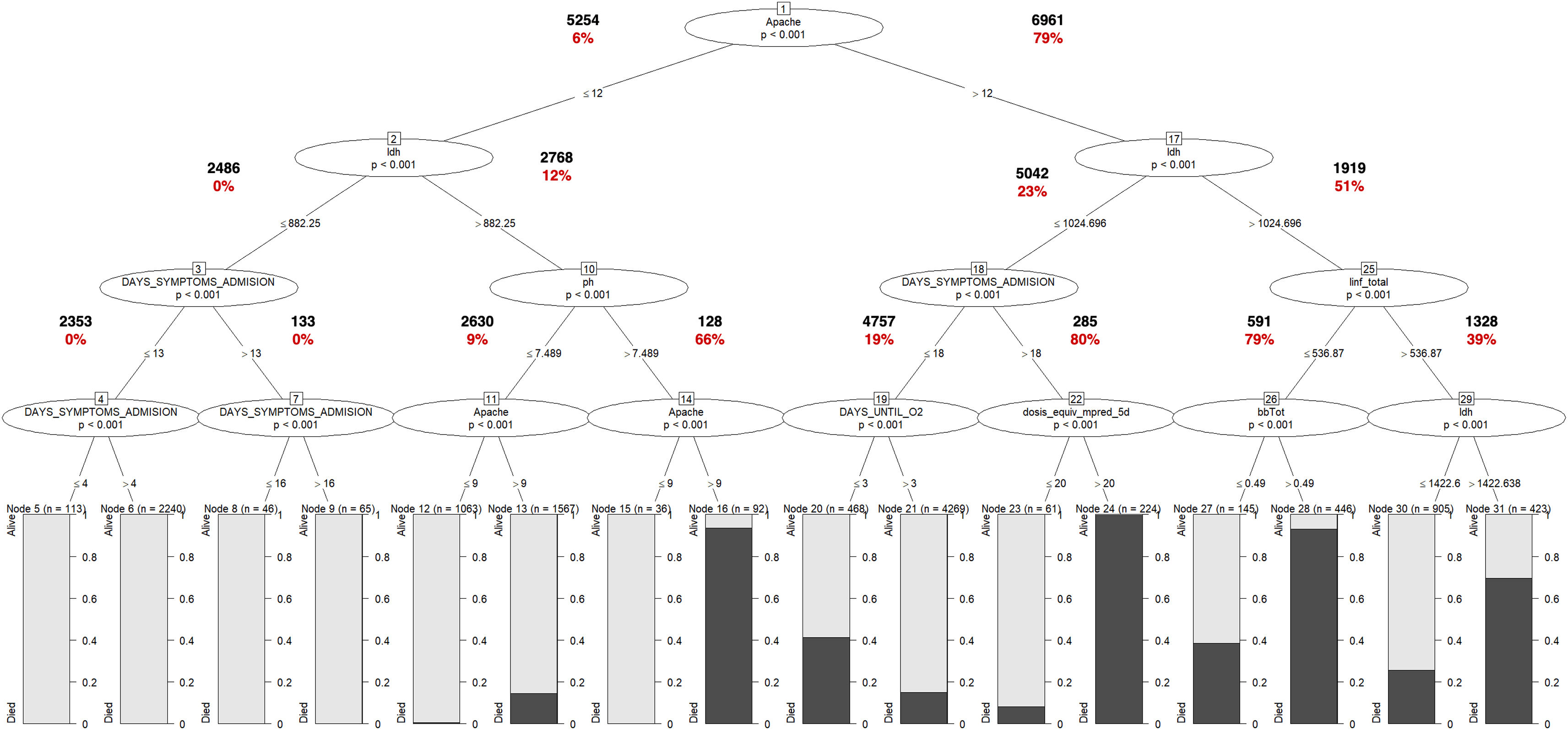
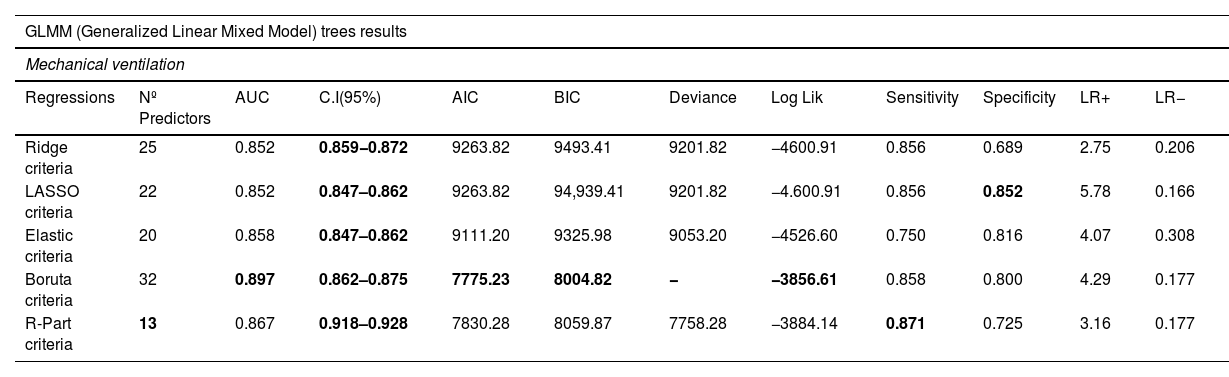
Modeling performanceIn Table 3, the performance of the IMV model is presented. The R-part predictors Regression-GLMTREE pair achieved the highest performance with an AUROC of 0.87, as shown in Figure 8 in the Supplementary material. Additionally, the ICU mortality model performed well, with an AUROC of 0.88, as demonstrated in Figure 9 in the Supplementary material. The IMV likelihood ratio (RV+ 3.16, RV- 0.177) suggests that the test result is moderately useful for identifying or discharge patients susceptible to being treated with IMV. Related to the CI (95%), the reached interval (0.918 and 0.928) suggests a high level of precision considering the sensitivity, specificity, and accuracy of the model. Related to ICU mortality, the IMV likelihood ratio (RV+ 5,105, RV− 0.424) and CI (95%) interval (0.817 and 0.833), results are also moderately useful. Fig. 3 illustrates the ICU Mortality decision tree, while Figure 7 in the Supplementary material presents the IMV decision tree. The optimal cut-off point for the prediction model was determined based on the IMV and ICU mortality AUC, using Youden's Index,26 which identifies the point of maximum sum of sensitivity and specificity in ROC curve analysis.
IMV Results.
| GLMM (Generalized Linear Mixed Model) trees results | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mechanical ventilation | |||||||||||
| Regressions | Nº Predictors | AUC | C.I(95%) | AIC | BIC | Deviance | Log Lik | Sensitivity | Specificity | LR+ | LR− |
| Ridge criteria | 25 | 0.852 | 0.859−0.872 | 9263.82 | 9493.41 | 9201.82 | −4600.91 | 0.856 | 0.689 | 2.75 | 0.206 |
| LASSO criteria | 22 | 0.852 | 0.847–0.862 | 9263.82 | 94,939.41 | 9201.82 | −4.600.91 | 0.856 | 0.852 | 5.78 | 0.166 |
| Elastic criteria | 20 | 0.858 | 0.847–0.862 | 9111.20 | 9325.98 | 9053.20 | −4526.60 | 0.750 | 0.816 | 4.07 | 0.308 |
| Boruta criteria | 32 | 0.897 | 0.862–0.875 | 7775.23 | 8004.82 | − | −3856.61 | 0.858 | 0.800 | 4.29 | 0.177 |
| R-Part criteria | 13 | 0.867 | 0.918–0.928 | 7830.28 | 8059.87 | 7758.28 | −3884.14 | 0.871 | 0.725 | 3.16 | 0.177 |
The Akaike Information Criterion (AIC) reports the information score of the whole models: the smaller the AIC value, the better the model fit. AIC is calculated from the number of independent variables to build the model and the maximum likelihood estimate of the model (how well the model reproduces the data). The best-fit model according to AIC is the one that explains the greatest amount of variation using the fewest possible independent variables. Bayesian information criterion (BIC) is another criteria for model selection that measures the trade-off between model fit and complexity of the model. A lower AIC or BIC value indicates a better fit. The log-likelihood (log Lik) value of a regression model is a way to measure the goodness of fit for a model. The higher the value of the log-likelihood, the better a model fits a dataset. Deviance is a goodness-of-fit metric for statistical models, particularly used for GLMs. It is defined as the difference between the Saturated and Proposed Models and can be thought as how much variation in the data does our Proposed Model account for. Therefore, the lower the deviance, the better the model. Sensitivity is the metric that evaluates a model's ability to predict true positives of each available category. Specificity is the metric that evaluates a model's ability to predict true negatives of each available category. The higher value of sensitivity would mean higher value of true positive and lower value of false negative. For the healthcare domain, models with high sensitivity will be desired. Specificity is the metric that evaluates a model's ability to predict true negatives of each available category. These metrics apply to any categorical model. Specificity is defined as the proportion of actual negatives, which got predicted as the negative (or true negative). Specificity is a measure of the proportion of people not suffering from the disease who got predicted correctly as the ones who are not suffering from the disease. In other words, the person who is healthy actually got predicted as healthy. The likelihood ratio is often used in statistical hypothesis testing and model selection to compare the fit of different models to the observed data. It is also commonly used in medical diagnostic testing to evaluate the diagnostic accuracy of a particular test or combination of tests. LR+ (likelihood ratio positive) is a statistical measure used to evaluate the diagnostic accuracy of a medical test. It is the ratio of the probability of a positive test result given the presence of the disease to the probability of a positive test result given the absence of the disease. In other words, the LR+ compares the likelihood of a positive test result in patients with the disease versus the likelihood of a positive test result in patients without the disease. In our case, a high LR+ indicates that the test is more accurate at correctly identifying patients how could need IMV, while a low LR+ suggests that the test is not providing strong evidence for IMV. By the way, LR− compares the likelihood of a negative test result in patients with the disease versus the likelihood of a negative test result in patients without the disease. A low LR- indicates that the test is more accurate at correctly identifying patients without the need of IMV, while a high LR- suggests that the test is not providing strong evidence for the absence of IMV. The LR+ and LR− are often used in conjunction with other measures of diagnostic accuracy, such as sensitivity, specificity to assess the overall performance of a medical test. It can help clinicians and researchers determine the optimal use of a particular test in diagnosing a disease or condition. CI stands for "confidence interval." A confidence interval CI is a range of values that is likely to contain the true value of a population parameter (such as a mean or a proportion), with a certain degree of confidence (usually expressed as a percentage, such as 95% or 99%). A narrower interval indicates greater precision, while a wider interval indicates greater uncertainty. The exact range of a "good" CI can vary depending on the context and the specific research question, but typically, a narrower interval is preferred as it provides a more precise estimate. In the case of the area under the receiver operating characteristic curve (AUROC), which is commonly used in binary classification problems, a CI that includes a value of 0.5 (indicating no discrimination between the two groups) is generally considered to be uninformative. On the other hand, a CI that does not include 0.5 and has a range of, for example, 0.7–0.8, may be considered good, indicating that the model has reasonably good discriminative ability. However, the interpretation of the AUROC and its associated CI should always be considered in the context of the specific research question and the particular field of study.
ICU Mortality Tree Predictors. The predictors appear in different branches attending to their significance in the predictive model. Values in bold letters represent the registries per branch. Values in red bold letters represent the percentage of registries with positive outcome. The variable named as “DAYS_SIMPTONS_ADMISION” is related with the number of days from first symptoms to ICU admission. The variable “linf_total”, is related to lymphocyte count per mm3. The variable named as “dosis_equiv_mpred_5d” is related with the corticosteroid dose, during the first five days of admission (mg of equivalent methylprednisolone dose). The variable named as “bbTot” is related with the total levels of bilirubin in blood. The variable names as “ldh” is related to the lactate dehydrogenase serum level. The variable DAYS_UNTIL_O2 is related to the number of days until the patient requires O2.
The trees in Figures 6 and 7 of the Supplementary material indicate that oxygenation status (ROX index) has the most significant influence on IMV, with a threshold near 5.2. On the other hand, ICU mortality is mainly influenced by comorbidities (APACHE II score) and LDH, as revealed by the same trees.
DiscussionThe results of the present study include some highly relevant clinical results. First, the variable sets predicting IMV, and ICU mortality are different. Whereas oxygenation variables are independent predictors of IMV, ICU mortality is associated with increased age and LDH and the presence of comorbidities. The latter variables may be considered markers of two processes: COVID-19-associated inflammation and ICU-acquired superinfection (see Figure 4 in the Supplementary material). Secondly, the characteristics of pharmacological therapy, including the administration of steroid drugs, has little influence on both the need for IMV and ICU mortality, considering our results. We included in the analysis 64 patients not receiving steroids and 216 receiving this treatment, at the usual 6mg dexamethasone or equivalent daily dose. This is a remarkable finding, because the effect of steroids on mortality identified in a previous trial27 have influenced recommendations, as well as clinical practice, since its publication. It may be speculated that the decision to include and randomize or not at the discretion of the attending physicians, and based on undisclosed criteria, rendered different results by selecting a study subset of COVID-19 cases with different characteristics. In comparison, no inclusion-exclusion criteria for selection process were applied in our “pragmatic” type of cohort. Steroids were given to almost every patient unless a severe contraindication existed, after the results of the RECOVERY trial were made available.
The present study applied a novel methodology (logistic regression with regularization plus GLMM Tree mixed models) to evaluate the relative importance of several variables as predictors of significant clinical events. Using machine learning and a fine-grained longitudinal multifaceted database, we have established relevant variable value thresholds to support clinical decisions. Although the model would perform quite well as predictor for IMV and ICU mortality, with good positive predictive values, it is important to emphasize that this is not a predictive model in the classical sense, but an attempt to pinpoint the most important clinical events that represent turning points during the studied process (in this case, clinical management of patients not initially under IMV). In this sense, we should say that the inclusion of the likelihood ratio as an evaluation factor for comparing performance model was reach great results. However, following the premise of model explainability, we believe it is important to take this element into account as a final selection factor for the set of predictors that best fit daily clinical practice. This study demonstrates that predictor-ranking methodologies using self-explainable machine learning may support therapeutic decision-making using observational data, when randomized clinical trials are unfeasible or unethical.
Regarding with the strengths of our study, we would like to mention the quantity and quality of the data set. Collected data have a high level of detail, leveraging the power of strategically devised electronic health records (EHR), which include relevant information in a highly structured and recoverable format. Every effort was made to configure our EHR to optimally gather all relevant information about COVID-19 patients. Also, our anonymized database is available in the repository along with the script we used for statistical analysis, is highly detailed and has been extensively curated to reflect temporal evolution and to improve data quality as much as possible. In any case, the collection of variables from Electronic Health Records (EHR) may be biased, affecting data quality. Age and gender biases are possible, as well as biases related to the selection and measurement of clinical variables. These biases can lead to incomplete or skewed representations of certain population groups and may impact the validity and generalizability of research findings and clinical decision-making. It is important to be aware of these biases to ensure proper interpretation and use of EHR data.
On the other hand, the limitations of our study results relate mainly to its single-centered nature and require confirmation in a multicenter dataset to gain external validity. Our methodology would be perfectly suited for a multicenter study, including “center” as a random factor in the second (GLMM Tree) part of the process. We suggest that future research applying this methodology could focus on designing clinical studies using observational data to answer relevant clinical questions without the logistic requirements of a randomized clinical trial or for hypothesis-generating purposes. Furthermore, when considering the limitations of using generalized linear mixed effects models (GLMMs) for modeling causation in critical care medicine research, it is important to highlight the absence of explicit causality assumptions. GLMMs primarily focus on association or correlation analysis, lacking the ability to address the assumptions necessary for establishing causal relationships. Specifically, GLMMs do not provide frameworks for the identification of causal effects or account for unmeasured confounding variables, which are crucial considerations in causal inference. In contrast, causal inference methods, such as the potential outcomes framework, explicitly address these assumptions, offering a more comprehensive approach for investigating causality. Therefore, when establishing causal relationships between variables, researchers should carefully consider the limitations of GLMMs and opt for causal inference methods, which provide a more robust approach for investigating causality in critical care medicine research.
In conclusion, different variables predict IMV and ICU mortality in severe COVID-19 patients, suggesting that the therapeutic decision of when to use IMV has little impact on ICU mortality. Our methodology is a valid option to assess therapeutic decisions using observational data when randomized clinical trials are not feasible or ethical.
Author's contributionSM, MA and AN conceived the presented idea. SM and MA contributed equally as first authors. SM and MA developed the theory and performed the computations. AN conducted an independent literature search to identify potentially relevant studies. MS independently reviewed the search results to identify pertinent articles. MS, AN, TF and VY contributed to the interpretation of the results. SM, MA, AN, MS, FL and AC took the lead in writing the manuscript. All authors provided critical feedback and helped shape the research, analysis, and manuscript.
FundingThis research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflict of interestThe authors declare that they have no conflict of interest.
None.