To test the hypothesis that the degree and duration of alterations in physiological variables routinely gathered by intensive care unit (ICU) monitoring systems during the first day of admission to the ICU, together with a few additional routinely recorded data, yield information similar to that obtained by traditional mortality prediction systems.
DesignA prospective observational multicenter study (EURICUS II) was carried out.
SettingFifty-five European ICUs.
PatientsA total of 17,598 consecutive patients admitted to the ICU over a 10-month period.
InterventionsNone.
Main variables of interestHourly data were manually gathered on alterations or “events” in systolic blood pressure, heart rate and oxygen saturation throughout ICU stay to construct an events index and mortality prediction models.
ResultsThe mean first-day events index was 6.37±10.47 points, and was significantly associated to mortality (p<0.001), with a discrimination capacity for hospital mortality of 0.666 (area under the ROC curve). A second index included this first-day events index, age, pre-admission location, and the Glasgow coma score. A model constructed with this second index plus diagnosis upon admission was validated by using the Jackknife method (Hosmer-Lemeshow, H=13.8554, insignificant); the area under ROC curve was 0.818.
ConclusionsA prognostic index with performance very similar to that of habitual systems can be constructed from routine ICU data with only a few patient characteristics. These results may serve as a guide for the possible automated construction of ICU prognostic indexes.
Comprobar si el grado y duración de las alteraciones en las variables fisiológicas recogidas en la monitorización rutinaria en UCI durante el primer día de estancia, junto con pocos datos adicionales, proporcionan información similar a la obtenida con los sistemas tradicionales de predicción de mortalidad.
DiseñoEstudio observacional, prospectivo y multicéntrico (EURICUS-II).
Ámbito55 UCIs de Europa.
Pacientes17.598 pacientes consecutivos, ingresados durante 10 meses.
Intervencionesninguna.
Variables de interés principalesse recogieron manualmente datos horarios sobre alteraciones o “eventos” en la presión arterial sistólica, frecuencia cardiaca y saturación de oxígeno, para construir un índice basado en estos eventos y un modelo de predicción de mortalidad.
ResultadosEl índice de eventos el primer día fue 6,37±10,47 puntos y se asoció significativamente con la mortalidad (p<0,001), con una capacidad de discriminación (área bajo la curva ROC) para la mortalidad de 0.666. Se construyó un segundo índice que incluye este índice de eventos en el primer día, la edad, procedencia del ingreso y puntuación de la Escala de Coma de Glasgow. Un modelo construido con este segundo índice más el diagnóstico fue validado mediante el método jackknife (Hosmer-Lemeshow, H=13.8554, no significativo), con un área bajo la curva ROC de 0,818.
ConclusionesSe puede construir un índice pronóstico con rendimiento similar al de los sistemas habituales a partir de los datos de monitorización de los pacientes en la UCI junto a escasas características del paciente. Nuestros resultados pueden servir de guía para la posible construcción automatizada de índices pronósticos.
Information on vital signs, e.g., blood pressure (BP), heart rate (HR), and oxygenation (SaO2) is routinely gathered in the ICU by monitoring equipment. Nurses currently transcribe data from monitors onto paper records, a labor-intensive activity.
Mortality prediction systems are widely used in critical care medicine to evaluate the quality of care (predicted versus observed mortality) and predict the mortality/survival of individual patients. Moreover, any study of critical care patients requires the quantification of their severity of illness, and numerous severity scoring systems have been developed, notably the APACHE,1–4 SAPS,5–7 and MPM8,9 systems, scoring patients according to their type of disease, age, history of disease, and degree of alteration of laboratory (hematocrit, leukocytes, etc.) and physiological (SBP, HR, etc.) variables. The score for physiologic variables is usually based on the most severe alteration observed in the patient at admission or during a given time (often 24h), taking no account of the timing or duration of abnormalities.
The use of prognostic indexes imposes a substantial work load. According to Teres and Higgins,10 who used trained data collectors at the bedside, the main issue is keeping up with the flow of patients. The IMPACT project of the American Society of Critical Care Medicine estimated that one full-time data collector is needed for every 20–30 ICU beds.11 For this reason, many centers do not routinely use these indexes. Automation of these tasks would facilitate their generalized routine application.
In the Euricus II study,12 detailed information was gathered throughout the ICU stay of patients on alterations in routinely collected physiological variables ICU (BP, HR, and oxygenation), classifying them as a function of their degree and duration.
The aim of this study was to test the hypothesis that routinely recorded data on the degree and duration of physiological alterations during ICU stay can be synthesized and used to predict mortality, and that first-day information plus very few additional data offer similar information to that provided by traditional mortality prediction systems. The data analyzed in the Euricus II projects were collected manually, the usual method in ICUs. The development of automatic computer systems to construct an index would enormously reduce the high workload currently required.
MethodsThe data in this study were derived from the EURICUS PROJET,12–18 using the database of EURICUS II,12,13 a multi-center, randomized, and controlled research project designed to determine whether improved collaborative practices in the ICU have beneficial effects on intermediate (physiologic derangement) and final (mortality) outcomes of patients. The project (from 1997 to 1998) included 55 ICUs from different European states and had two components: one involved the training and instruction of nurses and physicians on collaborative practice and the other the daily use of two protocols. The first one, designed to increase the awareness of nurse–physician interactions, consisted of a decision tree related to hypoxia (oxygen saturation), diuresis, pulse, and (systolic) blood pressure for nurses to apply hourly in the titrated therapy cycle (monitoring-comparison-action). The second protocol guided and stimulated the daily exchange of complementary information between nurses and physicians.
ICU performance was measured by recording the clinical outcomes of consecutively admitted patients. During a 10-month period, clinical data were recorded by trained personnel on age, pre-admission location, SAPS-II measured severity of illness during first day of stay,6 admission diagnosis according to APACHE III classifications,3 daily nursing workload using Nine Equivalents of Nursing Manpower Score (NEMS),19 organ dysfunction/failure at ICU admission and at 24h using the Sequential Organ Failure Assessment Score (SOFA),20 events and critical events (see Annex 1), and discharge destination. Patients were followed until hospital discharge, and their survival status was recorded (ICU/hospital mortality). Readmissions were not analyzed.
Trained personnel collected clinical data and applied protocols and questionnaires. All participating staff attended training sessions in each country and had access to a detailed operation manual containing protocols and definitions.
The study was approved by the ethics committees of participating hospitals, who waived informed consent. Results of this randomized and controlled study were published elsewhere.12,13,21
EventsEvents were defined as abnormal physiologic values (SBP, HR, and SaO2). More detailed definitions of physiologic events are given in Annex 1.
Events were defined by two characteristics: (a) parameter value outside range of accepted values and (b) persistence of divergence from normality for a given time period. Events were classified as critical or non-critical according to their duration and degree of divergence from normality (Annex 1).
It was recognized that the ranges of normality may vary according to the patient and his/her clinical condition and that a fixed range of normality would often be incompatible with good clinical practice (e.g. SaO2 of >90% in a patient with chronic obstructive pulmonary disease). Consequently, the physician responsible for the patient defined the normality ranges for the parameters in each case. Nevertheless, the study protocol indicated a reference normality range for each parameter (previously indicated by a panel of experts) to reduce bias in the uniform definition of events. The frequency of changes to recommended ranges was recorded: low BP (<90mmHg) was changed on 8.6% of occasions, high BP (>180mmHg) on 1.3%, SaO2 (<90%) on 3.6%, low HR (<60bpm) on 25.3%, and high HR (>120bpm) on 24.7% of occasions.
Events data were collected from all patients. After calculation of the total number and duration of events, their relationship with ICU mortality was studied. An event <1h was considered to last 1h, given that incidents were routinely recorded on an hourly basis.
Before the present study, the relationship of mortality with number and duration of ICU events was analyzed in all patients,13 finding the mortality to be more closely related to the duration than number of events. Consequently, the mean durations of events were categorized into intervals (no events, 0–1h with events, 1–4h, and ≥4h with events), such that their duration was as similar as possible among different events and there was an adequate patient sample for each interval. The aim was to facilitate results interpretation and establish a possible basis for a simple-to-use scale or scales, because the relationship between ICU mortality and mean of duration of events is not linear.
The present study analyzed events on the first, second, and third ICU days.
Index construction and outcomesThe events index was based on the number, type, and duration of events, assigning each patient and each day with a score. The index was quantified as a function of the relationship with ICU mortality shown by each type of alteration (see Table 1). Coefficients were calculated by logistic regression analysis, with ICU mortality as dependent variable and mean duration of events (in intervals of: 0, 0–1, 1–4, and ≥4h) as independent variables. Coefficients were obtained by multiplying beta coefficients of the categories (in the logistic regression analysis) by 10 and rounding decimals to the nearest whole number. The events score was then calculated for each patient and for each day of stay, although the present article only considered the first, second, and third days of ICU stay, primarily focusing on first-day events. The first day was considered to end at midnight on the day of admission, at which time the second day was considered to commence.
Relation between ICU mortality and mean duration of events (categorized in intervals).
| Blood pressure events | Frequency | Mortality |
| Non-critical events | ||
| No events | 8774 | (4.6%) |
| 0–1h with events | 5269 | (17.3%) |
| 1–4h | 2402 | (33.4%) |
| Four or more hours | 308 | (53.9%) |
| Critical events | ||
| No events | 11,177 | (4.8%) |
| 0–1h with events | 3298 | (20.6%) |
| 1–4h | 1675 | (40.2%) |
| Four or more hours | 603 | (65.5%) |
| Oxygen saturation events | ||
| Non-critical events | ||
| No events | 12,035 | (7.7%) |
| 0–1h with events | 3833 | (25.6%) |
| 1–4h | 773 | (40.8%) |
| Four or more hours | 112 | (57.1%) |
| Critical events | ||
| No events | 13,938 | (8.1%) |
| 0–1h with events | 2038 | (33.4%) |
| 1–4h | 576 | (56.8%) |
| Four or more hours | 201 | (72.6%) |
| Heart rate events | ||
| Non-critical events | ||
| No events | 10,433 | (6.1%) |
| 0–1h with events | 4642 | (23.3%) |
| 1–4h | 1407 | (32.1%) |
| Four or more hours | 271 | (43.2%) |
| Critical events | ||
| No events | 12,202 | (6.8%) |
| 0–1h with events | 2635 | (26%) |
| 1–4h | 1357 | (36.3%) |
| Four or more hours | 559 | (49.7%) |
The events score was constructed by using the ICU mortality as the dependent variable, following a previously applied methodology13 that had explained almost all of the ICU mortality by the combination of ICU events, multiple organ dysfunction, and diagnosis. Accordingly, we used data on the events on each day of stay in the ICU and their relationship with ICU mortality in order to determine the coefficients for calculating events index scores. The hospital mortality, the more usual outcome measure, was considered in the other analyses and was used to construct a second index that integrated the events index with other variables (i.e., first-day events index score, Glasgow Coma Scale, previous location, and age, classified as in SAPS II), designated the “combined events index” (see Results section).
Annex II shows two examples of how to calculate the “combined events index” and the probability of hospital mortality.
Statistical analysisData are expressed as mean±standard deviation for continuous variables and absolute frequency and percentage for categorical variables. The Student's t test was used to compare two means. The Analysis of Variance (ANOVA) and Newman–Keuls test for multiple comparisons were applied to compare more than two means. The Pearson coefficient was used to evaluate associations between quantitative variables.
The relationship of hospital mortality with the events score and other variables was studied by logistical regression, creating dummy variables for categorical variables. Based on these results, two indexes were created: events index and “combined events index”. Scores for variables and intervals for their categorization were assigned as a function of the beta coefficients obtained in the logistic regression. The discriminatory ability of the models was evaluated by the area under the ROC curve.22
We analyzed the discrimination of several possible models and studied the improvements in discrimination obtained by the addition of new variables that can be easily introduced into ICU monitoring systems and are known to discriminate between survival and non-survival, being included in APACHE, SAPS, and MPM and other widely used models. The discrimination of the events index was improved by adding age, previous location, and GCS, yielding the “combined events index”. This index was completed by including the admission diagnosis (classified as in APACHE III), which can also be included in the monitoring system at ICU admission. This final model was selected as the main object of the present investigation and for validation studies.
The entire sample was used for the creation of the model, and cross-validation was performed by using a jackknife approach,23 dividing the whole sample into 10 mutually exclusive groups by random method; 10 different regression models were estimated, with each model excluding one group; each model was used to calculate predictions for the excluded group. Predicted risks for individual patients from the excluded groups were then compared with predictions based on the entire sample. In all cases, the same variables with identical codes were included in the equations. The area under the ROC curve was also calculated for the predictions obtained by the cross-validated method, and the Hosmer Lemeshow test was used to compare observed and predicted mortality. The SPSS statistical package and MedCalc statistical software were used for all analyses; p<0.05 was considered significant.
ResultsThe study included 17,598 patients from 55 ICUs. Data on events were available for 17,022 patients (Table 1). Patients characteristics are shown in Table 2.
Characteristics of study population.
| Characteristic | Study population (N=17,598) |
| Age (years) | 59.11±22.06 |
| SAPS II (points) | 31.17±8.42 |
| Type of admission | |
| Medical (%) | 48.6 |
| Elective surgical (%) | 24.7 |
| Emergency surgical (%) | 26.7 |
| ICU length of stay | 5.2±9.94 |
| ICU mortality (%) | 13.9 |
| Hospital mortality (%) | 20.6 |
The mean events index value for the first day was 6.37±10.47 points (range, 0–70 points). Events index values were significantly associated with ICU and hospital mortality: the mean value was 4.85±8.47 points for the 13,348 patients who survived hospital admission versus 12.47±4.66 points for the 3405 who did not (p<0.001) and was 5.05±8.68 points for the 14,446 who survived ICU stay versus 14.91±15.72 for the 2287 who did not (p<0.001).
The relationship with mortality was further explored by dividing the index into intervals: the 9205 patients with a first-day index score of 0 showed a hospital mortality rate of 12.9%, the 3487 with a score of 1–10 points, mortality of 20.6%; the 1,934 with 11–20 points, mortality of 30.9%; the 983 with 20–30 points, mortality of 38.4%; and the 784 with >30 points, a hospital mortality rate of 58.2% (χ2=1342, df=4, p<0.001). The events index was also significantly associated with age (r=0.118, p<0.001), SAPS II score (r=0.377, p<0.001), and GCS score (r=−0.207, p<0.001).
The index score significantly differed according to patient type, with 7.73±11.68 points for medical patients, 5.53±9.9 for emergency surgical patients, and 4.75±8.11 for elective surgical patients (p<0.001 by ANOVA; significant intergroup differences by Newman–Keuls test). Trauma patients were included as medical or surgical patients according to their need for surgery.
The discrimination capacity for hospital mortality, evaluated by the area under the ROC curve, was 0.666 for the first-day events index score and 0.776 for the SAPS II score. The discrimination capacity of the events index was markedly improved by the addition of some other variables: addition of age increased the area under the ROC curve from 0.66 to 0.709; addition of first-day GCS score increased it to 0.763; addition of previous location to 0.792 and addition of admission diagnosis to 0.816 (Table 3).
Analysis of discrimination capacity for hospital mortality evaluated by area under Roc curve for different models.
| Events index (EI) | 0.666 | (0.655–0.677) |
| EI+agea | 0.709 | (0.7–0.719) |
| EI+agea+GCSb | 0.763 | (0.754–0.772) |
| EI+agea+GCSb+previous locationc | 0.792 | (0.783–0.800) |
| EI+agea+GCSb+previous locationc+diagnosisd | 0.816 | (0.808–0.824) |
| SAPS II+EI+agea+GCSb+previous locationc+diagnosisd | 0.833 | (0.823–0.838) |
There were statistically significant differences in all cases (p<0.05) by Hanley–Mcneil method.
Based on the results of logistic regression analysis with hospital mortality as dependent variable, a second index was constructed (“combined events index”) that included the first-day events index, GCS, and age, classified as in SAPS II, but with scores assigned according to the logistic regression results. It also included the previous location of the patient and reason for admission, which were both classified as in APACHE III and scored as a function of the logistic regression results. The score assigned to variables or categories was based on the beta coefficients of the logistic regression analysis such that the events score was similar to the original (because the beta coefficient of the score was 0.04, coefficients of the categories of the other variables were multiplied by 25 and decimals were rounded to the nearest whole number). Table 4 shows the scores assigned to categories of the new index. Selection of additional variables (age, GCS, and previous location) was based on previous knowledge of their importance and on the considerable improvement in the discriminating capacity of the events index produced by their addition, with very little additional data collection workload.
Events+age+coma+previous location index.
| Events score | |
| Blood pressure events | Score |
| Non-critical events | |
| No events | 0 |
| 0–1h with events | 4 |
| 1–4h | 7 |
| Four or more hours | 8 |
| Critical events | |
| No events | 0 |
| 0–1h with events | 6 |
| 1–4h | 14 |
| Four or more hours | 23 |
| Oxygen saturation events | |
| Non-critical events | |
| No events | 0 |
| 0–1h with events | 3 |
| 1–4h | 5 |
| Four or more hours | 6 |
| Critical events | |
| No events | 0 |
| 0–1h with events | 7 |
| 1–4h | 15 |
| Four or more hours | 17 |
| Heart rate events | |
| Non-critical events | |
| No events | 0 |
| 0–1h with events | 5 |
| 1–4h | 6 |
| Four or more hours | 6 |
| Critical events | |
| No events | 0 |
| 0–1h with events | 4 |
| 1–4h | 6 |
| Four or more hours | 10 |
| Age | |
| <40 years | 0 |
| 40–59 years | 10 |
| 60–69 years | 17 |
| 70–74 years | 24 |
| 75–79 years | 27 |
| >80 years | 33 |
| Glasgow Coma Scale | |
| 14–15 points | 0 |
| 6–13 points | 16 |
| <6 points | 46 |
| Previous location | |
| Elective surgery | 0 |
| Emergency | 12 |
| Emergency surgery | 13 |
| Other Hospital | 17 |
| Other Ward | 28 |
The “combined events index” showed a significant relationship with hospital mortality. The score was 65.76±28.53 points for the 3352 who died in hospital versus 37.51±21.54 for the 13,152 who survived (p<0.001); the mean score for all 16,504 patients was 43.25±25.77 points. There was also a significant difference in this index score between ICU non-survivors and survivors, with a score of 71.11±29.32 points for the 2250 who died in the ICU versus 38.85±22.16 for the 14,254 who survived (p<0.001).
We evaluated the relationship of the length of ICU stay with the SAPS II, events index, and “combined events index”, finding r=0.221 (p<0.001) with SAPS II, r=0.095 (p<0.001) with events index, and r=0.147 (p<0.001) with “combined events index”.
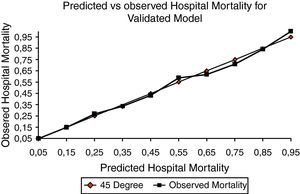
Finally, a hospital mortality prediction model was constructed and subsequently validated. It included the variables: the “combined events index”, the square of this index, and the admission diagnosis (Table 5). This model was validated by means of a Jackknife approach as explained above, using the same sample for the creation and validation of the model. The Hosmer Lemeshow test was applied to evaluate the discrepancy between the prediction of the cross-validated model and the observed mortality, giving a value of H=13.8554 (df 10), not statistically significant (Fig. 1). The discrimination capacity (area under the ROC curve) was 0.818 for the original model and 0.812 for the cross-validated one. This Jackknife-validated model differs from that shown in Table 3 under the heading “EI+Age+GCS+Previous location+Diagnosis”, because the latter does not include the square of the index score, which was added to improve the calibration.
Odds ratio of the final model.
| OR | ||
| Index | 1.053 | (1.046–1.06) |
| (Squared index)/100 | 0.989 | (0.984–0.994) |
| Most frequent diagnoses | ||
| Acute myocardial infarction | 0.231 | (0.14–0.381) |
| Bacterial pneumonia | 0.542 | (0.343–0.856) |
| Other respiratory diseases | 0.433 | (0.268–0.699) |
| Cranial trauma (with/without multiple trauma) | 0.252 | (0.155–0.409) |
| Medication poisoning | 0.059 | (0.031–0111) |
| Surgical diseases | ||
| Lung neoplasm | 0.117 | (0.065–0.209) |
| Gastrointestinal rupture/perforation | 1.257 | (0.780–2.025) |
| Gastrointestinal neoplasm | 0.637 | (0.333–1.217) |
For the diagnosis variable, cardiogenic shock was used as the reference category.
The information contributed by analysis of second- and third-day events was also studied. The mean events index score of patients was 7.17±11.49 points on the second day of admission (n=14,485) and 6.91±11.37 points on the third day (n=9570). When first-day events data were complemented with second-day events, by using the worst (highest) value for each patient in the first two days (or first-day data for patients with stay of 1 day), the area under the ROC curve increased from 0.666 to 0.716 (0.709–0.723), and when the worst value in the first three days was used it increased to 0.734 (0.728–0.741) (all differences, p<0.05; Hanley–Mcneil method). The area under the ROC curve increased to 0.765 (0.759–0.772) when first-day GCS score was included (in 3-day model), to 0.788 (0.781–0.794) when age was added, to 0.807 (0.801–0.814) when previous location was added; and to 0.831(0.825–0.837) when diagnosis was also added (all differences, p<0.05).
DiscussionThis study showed that a prognostic index that performs as well as the usual systems can be constructed from data already routinely recorded in the ICU complemented with a few characteristics of the patient and disease. One advantage of our index is that laboratory data are not required for its calculation. Although the data in the present study were manually collected, similar results could be expected by using the same data automatically gathered by ICU monitoring equipment. The results of this study may serve as a guide for a future automatization of the collection and use of prognostic indexes in the ICU.
An important component of this instrument is an events index that expresses the degree and duration of alterations in the HR, SBP, and oxygenation of the patient. Although the term “adverse event” is frequently utilized to describe injuries caused by medical management,24 it refers here to alterations in the above physiologic functions. Because numerous false alarms were expected,25,26 a 10-min time limit was established for recording abnormalities in physiological variables (events), reducing the number of false alarms and non-relevant events and excluding the extreme alterations observed when time limits are not imposed.
The variables used to calculate the “events index” (HR, SBP, SaO2) were selected because they were studied in considerable detail in the Euricus Project and because they are routinely recorded by bedside monitoring equipment in ICU patients, opening up the possibility of their automated collection. They were classified as critical or non-critical in the Project and therefore in the present study; the categorization of events and the scoring procedures were previously reported.13 This index evaluates not only the degree of an alteration but also, unlike other indexes, its duration. In fact, the discrimination capacity shown by this model was superior to that of SAPS II and similar to that of other prediction systems. Thus, although the area under the ROC curve was 0.81 for SAPS II in its reference population, it was 0.77 in our series, lower than the 0.82 obtained with our model. The model with “EI+Age+GCS+Previous location+Diagnosis+SAPS II showed a discrimination of 0.83. The difference between 0.81 and 0.83 may be explained by the additional information provided by the analytical variables (e.g., bilirubin, creatinine, platelets, and leucocytes) included in SAPS II but not in our model.
Importantly, our model also showed a good agreement between the predicted and observed mortality in the present series, with no significant difference according to the Hosmer Lemeshow test using a Jackknife approach (Fig. 1).
The manual collection of data from the documentation (charts, laboratory reports, etc.) for each patient, required by the usual prediction systems and indeed for our own index, imposes a heavy workload when systematically carried out in all patients. Even more effort and time must then be spent analyzing the data in order to estimate the likelihood of death for individuals and groups of patients. However, various researchers recently described computer systems for physiological data acquisition and analysis27–31 that offer complete information on the patient's clinical condition in the ICU. Bioengineering advances have led to an impressive amount of reliable data being available at the bedside,27,31,32 but clinical practice has yet to take full advantage of this rich, varied, and continuous stream of information, and the synthesis and interpretation of information is still performed manually in many ICUs, with minimal preprocessing.
Our original events data were gathered manually, before the possibility of constructing an index was conceived. Hence, these results can be generalized for manual but not automatic data collection systems. Moreover, we were unable to compare workloads between manual and automatic methods. Nevertheless, we believe that current bedside systems, with the appropriate settings, are capable of automatically gathering, analyzing, and transforming these data. They can be programmed for this purpose, entering the other variables considered in our study (age, pre-admission location, GCS score, and admission diagnosis [APACHE III classification]), and they can deliver highly valuable information, including the “combined index score” and likelihood of survival/mortality for each patient. A further advantage of an automated index is the reduction in inter-observer variability, which can influence mortality prediction.33
Our intention was not to replace existing indexes,1–9 since the manual collection of data on the degree and duration of these alterations implies a heavier work load. However, these routinely collected data appear to offer similar information to that provided by these systems, and future technological developments may vastly reduce the work involved in constructing this new type of index.
There have been reports on systems that use monitoring equipment software for vital constant analysis and mortality predictions. The Vanderbilt University group demonstrated that HR variability is a good predictor of mortality in trauma patients as early as 12h after admission and throughout ICU stay.34–36 Correlations have also been reported between HR variability and severity of illness and outcome in critically ill and injured children37 and diverse populations of critical ill patients.38 In the present study, mortality was found to be related to the alteration of three vital constants and to the duration of the alteration, allowing all three to be used in a prognostic index with an acceptable discrimination capacity.
Attempts have been made to develop an automated severity of illness and mortality risk system using data available in hospital electronic databases, e.g. the Veterans Affair Healthcare system, a model with a good discrimination and calibration.39 This experience supports the development of automated ICU risk prediction systems.
Tarassenko et al.40 recently published a system based on automated vital sign acquisition for intelligent alerting in patients with redeemable morbidity or avoidable mortality, further indicating the possibility of new prediction targets with this approach.
One study limitation is the possible influence on the results of the ability of the physician-in-charge to change the normality limits established for the physiological variables. In fact, they were respected in the large majority of cases, and changes were at the limits of normality, suggesting that a large proportion of ICUs considered these limits to be clinically useful.
The variables comprising the first-day events index (HR, SBP, SaO2) showed a low predictive value (area under ROC curve of 0.66) in comparison to other variables in the predictive system (age, previous location and Glasgow scale score, etc.). However, the latter also carry considerable weight in the usual severity indexes (SAPS, APACHE), and we do not consider this to be a study limitation. It may indicate that severity indexes that do not include these variables and rely solely on monitoring values may not perform as well as the habitual systems.
It is highly likely that the discrimination capacity of our index can be further improved after a period of implementation and research into the complementary use of other prognostic factors. Our study demonstrates that an automated system can be designed by taking into consideration the selected findings. Nevertheless, the effective functioning and usefulness of this approach can only be established after its application and validation in different populations. It is also necessary to test in practice our claim that it would significantly reduce the workload required by the commonly used prognostic systems and produce an economic saving that justifies its implementation.
FundingThis study forms part of the EURICUS project and was supported by European Union grant BMH4-CT96-0817.
Conflicts of interestThe authors have no conflicts of interest to declare.
| EVENT (Ev) | Critical event (CrEv) | |||||
| Suggested range | Continuously out-of-range | Intermittently out-of-range | Continuous event | Discontinuous event | Event anytime | |
| SBP(a) (mmHg) | 90–180 | ≥10′ | ≥10′ in 30′ | ≥60′ | ≥60′ in 2h | <60 |
| SaO2(b) | ≥90% | ≥10′ | ≥10′ in 30′ | ≥60′ | ≥60′ in 2h | <80% |
| HR(c) (bpm) | 60–120 | ≥10′ | ≥10′ in 30′ | ≥60′ | ≥60′ in 2h | <30 or >180 |
The normal range indicated in the protocol was 90–180mmHg. SBP was recorded hourly, and it was noted whether the measurement was made continuously or discontinuously (e.g., with sphygmometer).
A non-critical blood pressure event was recorded when: (a) SBP remained out of range for ≥10min (hypo-hypertension); (b) SPB was out of range for a total of ≥10min during a 30-min period if SBP was unstable and out of accepted range for periods of <10min. A Critical Blood Pressure event was recorded when: (a) SPB event lasted for ≥60min; (b) SBP event lasted a total of ≥60min during a 2-h period if SBP was unstable and out of range for <60min; or (c) SBP was <60mmHg (any duration).
The normal range according to the protocol was >90%. SaO2 was recorded when blood gas analysis was performed, or hourly in cases of continuous monitoring (e.g. pulse oximeter). In case of discontinuous monitoring, the occurrence of the event is defined by one measurement of SaO2 below range.
In continuous monitoring: (a) SaO2 remained below accepted value (hypoxia) for ≥10min; or (b) was below this value for a total of ≥10min during a 30-min period if SaO2 was unstable and below this value for periods of <10min. During artificial lung ventilation, SaO2 can fall below the accepted value due to care procedures (e.g. endotracheal suction). Therefore, the time factor for a hypoxia event in these cases was only considered after completion of these procedures (e.g., after re-connection of patient to the mechanical ventilator). In discontinuous monitoring (e.g., at blood gas analysis), the time factor was omitted and the event was exclusively defined by a measurement below the accepted value.
In continuous monitoring: (a) The event lasted ≥60min; (b) the event lasted a total of ≥60min during a 2-h period if the SaO2 was unstable and events lasted <60min; or (c) SaO2 was <80% (any duration). In discontinuous monitoring: (a) SaO2 was below the accepted value at two consecutive measurements, or (b) SaO2 was <80% at one measurement.
The normal range according to the protocol was 60–120bpm. HR was recorded hourly, and it was noted whether the measurement was made continuously (ECG lead) or manually.
A non-critical heart rate event was recorded when: (a) HR remained out of range (brady-tachycardia) for ≥10min; or (b) HR was out of range for a total of ≥10min during a 30-min period if HR was unstable and out of range for periods of <10min. A critical heart rate events was recorded when: (a) event lasted for ≥60min; (b) event lasted for a total of ≥60min during a 2-h period if HR was unstable and out of range for periods <60min; or (c) HR was <30bpm or >180bpm (any duration).
Depending upon their clinical condition, patients may have more than one critical event on the same day. It was therefore necessary to define the recovery period after one critical event was ended and before the next event was registered, as follows: SBP within accepted range for >60min; SaO2 within accepted range for >60min; HR within accepted range for ≥60min.
Example 1 As reported in annex 1 and the accompanying table, in a 66-year-old patient under continuous SBP monitoring, an SBP <90 but ≥60mmHg for <10min is not considered an event and the duration is therefore 0; when the duration of this episode is >10min but <60min, it is considered a non-critical event with a duration of 1h and an events scale score of 4 points (see Table 4). The patient shows a fall in SBP to below 90mmHg, the lower limit of the range, at 3h 20min, and then returns to within the accepted range at approximately 4h 10min, still not considered a critical event. The SBP again falls to below 90mmHg at 4h 20min and stays there for approximately 10min, therefore the total time with SBP <90mmHg during a 2-h period is around 1h (period 1+period 2). During the next three hours, the SBP fluctuates and is outside the accepted range for ≥60min. Hence, the events score for this patient is 23 points for a critical event of ≥4h (see Table 4). The patient shows no further events and is admitted from the Emergency Area for traumatic brain injury with a Glasgow Coma Scale of 5 points, being assigned a score of 98 points on the “Events+Age+Coma+Previous location” index, (Events, 23; Age, 17; Coma, 46; Previous location 12).
In order to calculate the probability of hospital mortality, we first compute the logit:
Logit=Constant+[0.051×(event+age+coma+previous location index)]+[−0.114×(events+age+coma+previous location index)×(events+age+coma+previous location index)/100]+diagnosis coefficient.
In this case:
Logit=−2.543+(.051×98)+[(−0.0114×98×98)/100]+(−1.379)=−0.0189.
This logit is converted to the probability of hospital mortality by the following equation:
Probability of hospital mortality=exp(logit)/[1+exp(logit)]. Hence, in this case, the probability of hospital mortality is 0.4953 (49.53%).Example 2 A 45-year-old patient is admitted to the ICU after elective surgery (lung neoplasm) with a Glasgow outcome scale of 15 points, oxygen saturation values always >90, SBP always 90–180 and HR always 60–20 except for a 5-min period above 120 before returning to 60–120. The events score for this patient is 0 points and the “Events+age+coma+previous location” index score 10 points (events, 0; age, 10; GCS, 0 points; elective surgery, 0 points).
In this case:
Logit=−2.543+(0.051×10)+[(−0.0114×10×10)/100]+(−2.150)=−4.295.
Probability of hospital mortality=exp(−4.295)/[1+exp(−4.295)]=0.0135.
Hence, the probability of hospital mortality is 1.35%.