In this review the usual methods applied in systematic reviews and meta-analyses are outlined. The ideal hypothesis for a systematic review should be generated by information not used later in meta-analyses. The selection of studies involves searching in web repertories, and more than one should be consulted. A manual search in the references of articles, editorials, reviews, etc. is mandatory. The selection of studies should be made by two investigators on an independent basis. Data collection on quality of the selected reports is needed, applying validated scales and including specific questions on the main biases which could have a negative impact upon the research question. Such collection also should be carried out by two researchers on an independent basis. The most common procedures for combining studies with binary outcomes are described (inverse of variance, Mantel-Haenszel, and Peto), illustrating how they can be done using Stata commands. Assessment of heterogeneity and publication bias is also illustrated with the same program.
En esta revisión se detallan los métodos habituales que se aplican en una revisión sistemática con metaanálisis. La hipótesis ideal para una revisión sistemática es la generada por el material científico que no formará parte del metaanálisis. La selección de los estudios supone la búsqueda en más de un repertorio en la web. Es obligatoria una búsqueda manual en la bibliografía de artículos, editoriales, revisiones, etc. La selección de los estudios debería hacerse por 2 investigadores independientes. Hay que reunir información sobre la calidad de los estudios, aplicando escalas validadas en las que deben constar preguntas específicas sobre los sesgos que pueden amenazar a la pregunta de investigación, por 2 investigadores independientes. Se describen los métodos más comunes para combinar estudios con efectos binarios (inverso de la varianza, Mantel-Haesnzel y Peto), y se muestra cómo hacerlo con comandos de Stata. La valoración de la heterogeneidad y del sesgo de publicación se ilustran con el mismo programa.
The term “meta-analysis” was created before the concept of systematic review. It was coined by Glass in 19761 to define a pool of statistical procedures to combine the results of several studies addressing the same research question. The Cochrane Collaboration defines “systematic review” as the synthesis of the results of several primary studies using techniques which decrease the risk of both bias and random error.2 The unit of research is not the individual, but the research study. Currently, meta-analysis is restricted to the data analysis of a systematic review.
In theory, a systematic review can be applied to any research question, either on etiology (e.g., the association between body mass index and clinical outcome for patients with acute respiratory distress syndrome3), diagnosis (e.g., the assessment of diagnostic accuracy of urinary TIMP-2·IGFBP7 for acute kidney injury in adults4), prognosis (e.g., high-flow nasal cannula oxygen therapy in adults with acute hypoxemic respiratory failure5) or any intervention, either preventive (e.g., prone position ventilation in patients with acute respiratory distress6) or therapeutic (e.g., the use of fibrinolytics in acute myocardial infarction – AMI-7). The general objectives of a systematic review can be:
- 1.
The assessment of consistency (or its absence, that is, presence of heterogeneity) across the primary studies; for instance, the treatment with fibrinolytics in AMI was highly heterogeneous across 33 studies, being due mainly to the delay in using the drug.7
- 2.
To obtain an overall estimator of an association. In the meta-analysis of fibrinolytics, the pooled odds ratio – OR – was 0.83, highly significant (p<0.001).7
- 3.
To identify the subgroups where an exposure (a test, treatment, etc.) shows a higher or lower strength of association. Fibrinolytics increase AMI mortality in the short term (first 48h), although it is widely outweighed in the long term.7 Meta-analysis failed in identifying any subgroup at an increased risk of death in the short term.8
- 4.
The assessment of quality of the primary studies to offer a guide for future studies on the subject.
The outline of a systematic review is as follows9:
- 1.
A research question based on a hypothesis.
- 2.
Selection of the study population (primary studies):
- (a)
Sources of data.
- (b)
Search criteria and inclusion criteria.
- (a)
- 3.
Data collection: assessment of the validity of primary studies and extraction of relevant data.
- 4.
Meta-analysis:
- (a)
Statistical methods to combine data.
- (b)
Assessment of heterogeneity in the pooled estimates.
- (c)
Ascertainment of publication bias.
- (a)
It is important to remember that a basic principle of research is that a hypothesis cannot be proved using the sample which suggested it. This is very common in systematic reviews, where investigators read some studies, note that they are not consistent (no firm recommendation can be derived from them) and decide to carry out a systematic review, in which the studies which gave the idea are also included in the meta-analysis. This procedure caused in the past rejection of meta-analysis as a method of research by prestigious scientists.10
The ideal situation is that the hypothesis would be originated in a sort different of research. For instance, in the association between garlic intake and risk of cancer the idea was suggested by experimental studies on rats fed with a diet enriched in garlic11: this launched a search of epidemiologic studies in humans to assess the relationship.
Selection of the study populationSearch of studiesGeneral strategiesThe reference population in a systematic review are all the researches carried out on a subject in the world. There are several strategies:
- 1.
To search all the available information, either published or not. To get unpublished studies is not easy. As an approach, a researcher can consult theses, grants and projects funded by agencies (governmental and private), presentations at scientific meetings, interviews to specialists on the topic, etc. This strategy tries to minimize publication bias.
- 2.
To search published studies only: it is the most common. It saves time and money versus the previous strategy. However, it is prone to publication bias, if the published studies do not represent all the performed researches.
- 3.
To use the original databases of the identified primary studies. Its main advantages are a better adjustment of confounding bias and assessment of interaction (if an exposure changes its effect according to other variables). Its drawback is that some authors do not like to share their data.
The most usual search methods, which should be used combined, are the next:
- 1.
To search in web repertories of journals. There are many, some of them specialized on some topics (cancer, toxicology, etc.), territories (SCIELO, Latin-American countries), health professions (CINAHL on nursing), etc. The most popular is PubMed (US National Library), but it is not enough. EMBASE should also be searched out. Today the ISI Web of Knowledge (Institute of Scientific Information, USA) includes several databases and repertories of meetings and doctoral theses. SCOPUS (Elsevier), which includes PubMed, EMBASE, conference proceedings and books, is a very important resource. The last two sources are free for all Spanish universities.
- 2.
A handsearch of the references of all primary studies, editorial, reviews, etc., identified in the electronic search, is compulsory.
- 3.
To interview investigators on the topic. It can help in identifying unpublished studies and to update published results.
- 4.
Other sources: proceedings of scientific meetings, national repertories of doctoral theses (such as the Spanish TESEO database), grey information (such as reports made by governmental agencies), etc. These sources are mainly used to identify the variables associated with publication bias.
They should be established before knowing the results of the primary studies and applied by two researchers independently to avoid selection bias.12–15 Some criteria may require to be judged to get the full publication and not the abstract only:
- 1.
Language: It is very common in native English authors to restrict their search to studies published in English. We, in our first published meta-analysis on oral contraceptives and cervix cancer, selected studies published in the languages of America and Western Europe (English, Spanish, Portuguese, French, German, and Italian).16 Currently, this is not an acceptable conduct as publication bias can be caused by language. If a report is found in another language it should be translated by a professional in scientific writing (it is misleading other approaches, such as translation programs or native lay persons who do not know scientific language), although it increases the costs. If one researcher wants to carry out a review on the studies performed in one geographical area could restrict the language; e.g., if the research question is on chemoprevention and risk of neoplasm, a search will give many reports written in Chinese. There are two options: to include a Chinese investigator or to focus on the studies done in Western countries (as an additional inclusion criterion), as it is very unlikely that an American, French, etc., author publishes his results in Chinese, Korean, etc.
- 2.
Type of design: In pooling clinical trials it is usual to restrict selection to randomized trials, due to their higher validity (very common in the Cochrane Collaboration). In meta-analyses of observational studies, ecological studies are commonly discarded by the unpredictable effects of ecological fallacy.
- 3.
Characteristics of exposure and outcome: Correct definitions of the exposure (even treatments are variable in timing, dose, etc.) and outcomes (single or combined) are needed for proper analyses.
- 4.
Type of publication: It should be centered on original reports. Reviews, letters, abstracts and editorials should be discarded, as the methods cannot be assessed adequately.
- 5.
Quality: This item requires evaluation of the full report and will receive attention in the next epigraph.
Information on aspects relevant to quality of the research should be obtained before gathering quantitative data to be pooled in meta-analysis. It has been said that meta-analysis cannot improve the quality of original studies. Therefore, researchers should be aware from the beginning whether the results of a report are menaced by bias. Data gathering should be done by two reviewers independently,13–15 as it is very unlikely that a published report allows to get a definite answer on many methodological aspects. They should discuss their results if they are inconsistent. A third investigator will resolve the doubts. Researchers can also contact corresponding authors of primary studies for details not addressed in the published report and/or for an update of the results.
Assessment of study qualityMost researchers apply a published scale to assess the quality of a report. Most systematic reviews are based on clinical trials. The first scale to grade quality of controlled clinical trials was confectioned by Thomas Chalmers et al. in 198117 (four pages, 37 items). From then many scales (>60) have been developed for trials. The most used is that of Jadad et al.,18 because of its simplicity: just three questions on randomization, blinding and withdrawals, scoring up to 5 points. The Jadad scale has been a standard in Cochrane reviews, demanding a score of at less 3 to include a study.
We have many reservations about using a cutoff point on a scale to select a study. For example, suppose a study with adequate randomization, analysis of drop-outs, but not blinded, being the assessment of outcome influenced by a researcher when he knows the exposure status. The score according to Jadad's scale will be 3, but is subjected to bias.9 That means that a likely biased study could be considered as adequate. There are important reports on the consequences of adopting cutoff points in scales to select studies. Jüni et al.19 used 25 scales to grade trials in the comparison of two types of heparin (low molecular weight heparin and normal), classifying the studies as of low or high quality according to each scale: when they pooled the studies of low and high quality of each scale, they reached contradictory results; with some scales high quality studies yielded better results for low molecular weight heparins than for normal ones, and the contrary with other scales.
The former leads to the fact that a quality questionnaire must include specific questions on the main biases which menace a research question. It is relatively easy to develop a quality scale on trials. On observational designs the situation is very different. Standardization is difficult. Nevertheless, many efforts have been made. Presently, two general questionnaires are applied for these designs. The first is the Newcastle-Otawa scale20 and the second is the STROBE statement21; it should be remembered that they are general questionnaires, and that for a proper evaluation of bias, specific questions on the main limitations to be avoided should be added. For example, when we did our meta-analysis on oral contraceptive use and cervix cancer, we included questions on the main biases on this relationship.22
Should be blinding applied in the assessment of study quality? It is not needed according to the manual of the Cochrane. We do not share this opinion as there are in epidemiology an unsurmountable number of reports on information bias: how people can influence their answers by previous knowledge. Researchers can be influenced by countries (USA is equal to Slovenia?), institutions (Harvard or Jaen?), prestige of authors, etc. If the reviewers of quality are pristine (e.g., students of epidemiology) there is no problem (it has been used in Harvard), but if the reviewer is an experienced researcher he should be blind to avoid bias. To do this use a scanner, digitize the paper, discard all the filiations and proceed to evaluation. Could a researcher in a field do a systematic review? Of course. However, he may have privileged information on some studies and both study selection and quality assessment may be biased. It would be advisable in these situations that neutral data collectors, according to a written protocol, carry out these tasks.
The usefulness of a quality questionnaire is not to obtain an overall quality score, but to get data on methodological details of a study, procedures applied to decrease bias, and so on. These data can be used later to justify heterogeneity among studies.
Meta-analysisWe will describe the methods for combining published studies. (If databases are pooled in one file, statistical analyses are conventional with the recommendation of including a new variable – the name of study – in multivariable models.) This can be accomplished by several programs, specific for meta-analysis (such as the Review Manager of the Cochrane, or Comprehensive Meta-analysis), or included in general statistical programs (SAS, R or S-Plus, SPSS, and Stata). We prefer the latter ones as they allow to do conventional analyses in the same database.
The main idea to pool data from several studies is the concept of weighted mean. Any mathematical procedure applied to combine data needs two figures from each study: a parameter, θi, and a weight, wi. Then, a weighted average or pooled estimate is computed: θp=(∑wiθi)/∑wi.
Methods for binary variablesMost published meta-analyses deal with binary variables and follow the notation shown in Table 1. In this table several parameters can be calculated: relative risk (RR), odds ratio (OR) and risk difference (RD). The equations to estimate them are detailed in Table 2, where also the formulae to calculate their variances are given. The parameter most often estimated in meta-analysis is the OR, which conveys the same meaning of RR. One important difference between RR-OR and RD is that the former do not follow a lineal scale, but exponential. This means that a variance for RR and OR can only be estimated if logarithms are taken.
Notation of a study with binary variables (exposure and outcome).
| Outcome+ | Outcome − | Total | |
|---|---|---|---|
| Exposure + | a | b | n1 |
| Exposure − | c | d | n0 |
| Total | m1 | m0 | ni |
Note: this notation can serve for several designs: (a) cohort, being n1i and n0i the exposed and the non-exposed, respectively; (b) controlled trial, being n1i and n0i the experimental and control groups; or (c) case–control, being m1i and m0i the groups of cases and controls.
In this situation the weight is the IOV of the parameter. If OR or RR is chosen, that means that the parameter to be pooled is the logarithm (OR) or logarithm (RR). After pooling, the antilogarithm (or exponentiation) will be applied. Some statistical programs do by default the transformation, but others do not. The IOV method can be used for both raw data and multivariate-adjusted parameters.
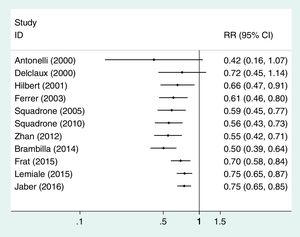
In Table 3 we reproduce a published meta-analysis24 on the comparison between application of non-invasive ventilation and standard oxygen therapy in adults with acute hypoxemic non-hypercapnic respiratory failure.
Meta-analysis on the comparison between application of non-invasive ventilation (NIV) and standard oxygen therapy (SO) in adults with acute hypoxemic nonhypercapnic respiratory failure; the outcome is intubation rate.24
| Author year | NIV (intubation) | SO (intubation) | RR (95% CI) | ||
|---|---|---|---|---|---|
| Yes (aa) | No (b) | Yes (c) | No (d) | ||
| Antonelli 2000 | 4 | 12 | 9 | 6 | 0.42 (0.16–1.07) |
| Delclaux 2000 | 15 | 25 | 18 | 23 | 0.85 (0.50–1.45) |
| Hilbert 2001 | 12 | 14 | 20 | 6 | 0.60 (0.38–0.96) |
| Ferrer 2003 | 12 | 24 | 26 | 13 | 0.50 (0.30–0.84) |
| Squadrone 2005 | 1 | 104 | 10 | 94 | 0.10 (0.01–0.76) |
| Squadrone 2010 | 2 | 18 | 14 | 6 | 0.14 (0.04–0.55) |
| Zhan 2012 | 1 | 20 | 4 | 15 | 0.23 (0.03–1.85) |
| Brambilla 2014 | 6 | 34 | 26 | 15 | 0.24 (0.11–0.51) |
| Frat 2015 | 55 | 55 | 44 | 50 | 1.07 (0.80–1.42) |
| Lemiale 2015 | 73 | 118 | 82 | 101 | 0.85 (0.67–1.09) |
| Jaber 2016 | 49 | 99 | 66 | 79 | 0.73 (0.54–0.97) |
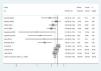
The IOV can be applied in two ways: as a fixed-effects model FEM or a random-effects model (REM). The FEM is based on the assumption that all the existing studies have been collected, and this implies that there is no sampling error. On the contrary, the REM departs from the fact that not all the studies could be located, so meta-analysis pools a sample of studies. That is why in the weight of this model two terms are considered: one is the intra-study variance and the other is the sampling error, or between-study variance, which increases the overall variance of the REM. If there is not sampling error the REM simplifies to the FEM. The pooled RR with REM for example of Table 3 is 0.60 (95% CI=0.45–0.79), p=0.001; whereas the results with the FEM are RR=0.75 (95% CI=0.66–0.85), p<0.0001.
The relative weights for each study in the two models are displayed in Table 4. One relevant conclusion derived from the weights is that the relative influence of each study on the pooled RR changes; e.g., the heaviest study with the FEM is that of Lemiale, which has 1.5 times more influence than the study by Frat. With the REM the differences between the weights decrease and the two studies show a similar weight. That is thought to be serious limitations of the REM which gives more importance to small studies, more prone to publication bias (see in Table 4 that the small studies have more weight in the REM). Another criticism raised with the REM is that while a standard error has a biological meaning (is the root square of the variance: mean of the quadratic differences of the series regarding the mean), the between-study variance has no biological interpretation.25
Weights for each study of the example in Table 3 using the inverse of variance method for the fixed effects model (FEM) and the random effects model (REM).
| Author year | Weights (%) for | Sample size | |
|---|---|---|---|
| FEM | REM | ||
| Antonelli 2000 | 1.96 | 6.01 | 31 |
| Delclaux 2000 | 6.26 | 10.93 | 81 |
| Hilbert 2001 | 8.08 | 11.94 | 52 |
| Ferrer 2003 | 6.67 | 11.19 | 75 |
| Squadrone 2005 | 0.42 | 1.77 | 209 |
| Squadrone 2010 | 0.97 | 3.59 | 40 |
| Zhan 2012 | 0.40 | 1.67 | 40 |
| Brambilla 2014 | 2.93 | 7.67 | 81 |
| Frat 2015 | 21.52 | 14.89 | 204 |
| Lemiale 2015 | 30.00 | 15.54 | 374 |
| Jaber 2016 | 20.81 | 14.81 | 293 |
| Total | 100.00 | 100.00 | 1480 |
The method can very easily be computed with the statistical package Stata.26 The commands related to meta-analysis are not included in the program, although they can be discharged free from the Stata website. The command which does all the above analyses is metan. For binary variables metan works with 2, 3, or 4 variables. With 2 variables the 1st one is the parameter (if OR/RR is the logarithm of them) and the 2nd is the standard error; with 3, the 1st one is the parameter, the 2nd the lower limit of the CI, and the 3rd the upper limit; and with 4 variables, metan assumes to work with raw data in the order of Table 1: a (exposed cases), b (exposed non-cases), c (non-exposed cases), and d (non-exposed non-cases). If the FEM is demanded fixedi should be written in the options, and randomi for REM. When logarithms are introduced (2–3 variables), the option eform yields OR/RR in the output.
The default of the output of metan includes a forest plot, in which the parameter of each study is inside a box whose area is proportional to the weight of the study. The forest plot of the example of Table 3 is displayed in Fig. 1.
Forest plot of the meta-analysis carried out with the example of Table 3, fixed-effects model.
It is a procedure for raw counts (as in Table 1). The weight is the product of exposed non-cases by non-exposed cases divided by the sample size. It is appropriate when there is no confounding (mainly randomized trials). With the command metan MH is the default with a FEM. If a REM is wanted, the term random must be specified in the options. This method is more adequate than the IOV when data are sparse (low counts). One important fact to remember is that when a 0 count is found in exposed or non-exposed cases, metan adds 0.5 to each cell (a default). If this is not wished, the studies with 0 outcomes should be discarded previously or to use the option cc (continuity correction) writing cc(0).
Peto's method28It is also a method for raw data and uses the Peto's OR in which the expected exposed cases (versus the observed exposed cases, cell a in Table 1) in the exposed group is estimated using the incidence of cases in the whole study (exposed plus non-exposed). It is a FEM and a REM is not available. It is appropriate for trials with a balanced design in the experimental and control groups, and when OR is close to 1; under other circumstances the method can yield biased results.29 One of its advantages over the previous methods is to deal with 0 cases in the control group, although there are better methods using the Mantel-Haenszel's method30; they are implemented in the command mar, by Doménech (Universitat Autónoma de Barcelona) in his course on Systematic Reviews (http://www.metodo.uab.cat/indexDesktop.htm),9 but not in metan.
In meta-analysis several statistical methods can be applied on the same database. This is a form of sensitivity analysis. If all of them agree it is reassuring. In the example, IOV, MH and Peto give similar figures (results not shown). However, if disagreement is observed the assumptions of each method should be revised and taken into account for a decision. In this review we have not enough space to detail sensitivity analyses based on the correction of potential biases; about confounding, more useful for meta-analysis of observational studies, the method is described in Ref. 9.
Methods for continuous outcomesThat is the case, for example, of serum cholesterol levels after a treatment versus levels in a control group. In this situation the only method to be used is the IOV with its two options, FEM and REM. Here the command metan can works with 2, 3, 4, or 6 variables. With 2 variables the 1st is the mean difference and the 2nd its standard error; with 3 the order is mean difference, and its CI lower and upper limits; for 4 variables the order must be the mean of the exposed group, its standard error, and the same for the non-exposed group; and for 6 variables, mean of the exposed group, its lower and upper limits of the CI, and the same for the non-exposed group. The methods to estimate the pooled estimate are beyond the scope of this manuscript but a thorough review can be found elsewhere.31
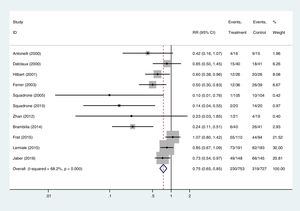
Cumulative meta-analysisIt is to carry out a meta-analysis adding in each step a new study which are ordered by a continuous variable. In this way, the influence of a study on the previous estimate is seen. The most common cumulative meta-analysis is by date of publication: studies are ordered by their year of publication (from the past) and the program does a meta-analysis adding each time a more recent study. A paradigmatic example is the meta-analysis by Lau et al.7 on fibrinolytics and mortality in AMI: it shows how a definite conclusion could have been reached in the 1980s, before the two megatrials (GISSI-I, ISIS-2) had been done, saving millions of deaths.
Other common variables used in cumulative meta-analysis are rate of the outcome in the control group (it is usual to see how the magnitude of effect decreases as the rate in the control group is higher), delay in applying an intervention, quality of the study, etc. It is useful to identify variables which could explain heterogeneity among the studies.
In Stata the command for cumulative meta-analysis is metacum. One important thing to remember is that the analyst has to order the studies in the database (commands sort and gsort). The options of this command are similar to metan. A cumulative meta-analysis of the data in Table 3 is displayed in Fig. 2. In this situation the image conveys the meaning that the first published studies obtained stronger associations than the later ones.
Cumulative meta-analysis, fixed-effects model, of the example shown in Table 3.
In meta-analysis it is very usual to read: “a FEM was carried out and if heterogeneity was significant a REM was applied”. This is an example of data torturing, and it is not serious, as investigators can select the model which agrees more with their beliefs. Heterogeneity and publication bias have a role in the election of the model; therefore, after commenting these aspects, it will be addressed.
HeterogeneityWith any program every calculated pooled estimate is accompanied with a heterogeneity test. The procedure implemented by all programs to detect heterogeneity is the χ2 of Cochran,32 later named as Q.33 It is a statistic which lacks statistical power and it is recommended that the significance level should be at least 0.1, instead of the classic 0.05. Today, the parameter I,2 the percentage of unexplained heterogeneity, is required in meta-analysis.34,35Metan provides these statistics in all analyses.
The presence of heterogeneity leads to think that the pooled parameter is obtained from studies which reach different conclusions. Suppose that you are said that the mean tall of Africans is 1.75, and that in Africa there are two races only, Watusis (mean tall 2m) and Pygmeans (mean stature 1.5m), 50% each; under these conditions, if one travels to Africa he will find that the mean stature he was said has no sense as there are two means. This is what happens when heterogeneity is detected: some studies may lead to different effect estimates. Thus, it is essential to identify the reasons behind it. To select variables which could explain heterogeneity, any researcher should be aware that they can be divided in two groups:
- 1.
Related to design:
- (a)
The design itself: cohort studies sometimes do not yield the same results of case-control studies; e.g., in a meta-analysis on cholecystectomy and risk of colon cancer the association was only supported by case-control studies.36
- (b)
Characteristics of the design: for instance, concealment of allocation in randomized trials does not support the results with open randomization lists.37 Validated questionnaires on diet do not yield the same results of non-validated ones on the association between fiber and colon cancer.38 There are many other examples.
- (a)
- 2.
Related to the study population
- (a)
Characteristics of the exposure: for example, in the meta-analysis of Lau et al.,7 the delay in treatment justified the heterogeneity.
- (b)
Type of outcome: in the previous cited meta-analysis on cholecystectomy and risk of colon cancer the association was appreciated for proximal colon cancer and not for distal cancer.36
- (c)
Modifiers of the relationship between exposure and outcome: e.g., Fine et al.39 found that the efficacy of pneumococcal vaccine was higher in hospitalized patients than for the general population.
- (a)
To explain heterogeneity several strategies of analysis can be applied:
- 1.
Stratified analysis: For instance, Bernal et al.40 found a strong heterogeneity in their study on the association between vasectomy and prostate cancer. They did a stratified analysis dividing the studies in two groups: one dealing with detection bias appropriately (people undergoing vasectomy are thoroughly explored) and the remaining. The association was seen in studies not addressing detection bias. This sort of analysis requires enough number of studies in each strata; it cannot be applied in meta-analysis with a low number of studies. The command metan allows to do stratified analysis with the option by.
- 2.
Meta-regression: It is the name for linear multivariable regression analysis applied to meta-analysis. The dependent variable is the parameter of each study (logarithms when OR/RR are of interest). It could be done by common commands of Stata weighting the studies by their variance, although there is specific command for meta-analysis, metareg. We recommend its use, as it allows to do Monte-Carlo simulations (permute option), very relevant when the number of studies is less than 10 and/or several variables are included in the model.
For instance, we did it in a meta-analysis on estrogen replacement therapy and risk of breast cancer, in which a highly significant heterogeneity was present. The inclusion of two variables (proportion of women receiving long-term treatment – >5 years – and proportion of current users) in the model yielded an r2 of 0.8, i.e. the two variables justified an 80% of the variability.41
- 3.
Cumulative meta-analysis: as already said this procedure allows to see candidate variables to be included in a formal meta-regression analysis.
- 4.
Influence analysis: this procedure tries to detect the study/ies causing heterogeneity. The analysis is repeated excluding the candidate studies. To detect them it is useful the forest plot given by default by metan, in which an outlier can be identified.
It is produced when the published studies do not represent all the researches carried out. Several determinants of publication bias have been identified: type of funding,42 conflict of interest,43 preconception,44 institution prestige,45 language of the journal,46 etc., but two variables are the most influential: statistical significance of the main result and sample size.42,47,48 On these variables most of the common procedures to detect publication bias are based upon.
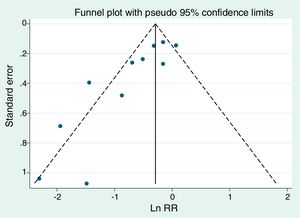
The simplest procedure to assess publication bias is the funnel plot. In the past the graphic could be horizontal and vertical, using the standard error or sample size. Today all funnel plots are vertical: in x-axis the parameter of each study and in the y-axis the standard error of the parameter. To discard bias the image should be symmetrical around of a vertical axis drawn through the pooled effect estimate. The Stata command for this is metafunnel. The funnel plot of the example in Table 3 is shown in Fig. 3. It is easy to see that there are studies with great figures of standard error on the left side, but not on the right, that is, the small studies suggest a stronger effect of non-invasive ventilation than the big ones.
Funnel plot of the example of Table 3.
It is convenient to assess the statistical significance of the presence of publication bias. Several procedures, based on regressions on different types of figures, are implemented in the command metabias of Stata: Begg,49 Egger,50 Harbord51 and Peters.52 According to simulation studies the best is that of Peters, although the most used is Egger. We have used metabias to assess the presence of publication bias (or small-study effects as preferred for Egger) in the example of Table 3. The Egger test requires in the varlist of metabias the parameter (remember the logarithm of OR/RR when they have been chosen) and its standard error, whereas for Peters test the raw data (cells a, b, c, d of Table 1) are needed. In the article of example 3 it is said that there is “no obvious publication bias”. The funnel plot is clearly asymmetrical; furthermore, the significant results for the tests of Egger (p=0.002) and Peters (p=0.03), not applied in the article, suggest the very opposite.
Another procedure, the “trim and fill”53,54 requires a different command, metatrim, also free in the Stata website. It is not very used, although, under asymmetry in a funnel plot, it allows to reconstruct a symmetrical image, assessing the consequences of bias.
There are other procedures, some of them to assess the number of non-significant studies needed to turn a significant association into a non-significant one; if the number is high it is very unlikely that all of them could be unpublished, but if the number is low (e.g., 1–3), the meta-analysis is very sensitive to unpublished reports.55 They are not implemented in Stata, although they can be run in the command mar, by Doménech.9
Heterogeneity and publication bias are important regarding the election between a FEM and a REM in meta-analysis. In Table 5 we give an outline about how to proceed.9,56–59
Questions to be considered in the election between a fixed effects model (FEM) and a random effects model (REM) (sources: 9,56–59).
| Question 1: the scope |
| Can treatment ever achieve benefit? FEM |
| Will the treatment produce benefit ‘on average’? REM |
| Question 2: ‘universal sample’ |
| Are you ‘sure’ that all the existing studies, either published or not, have been located? |
| Yes: FEM |
| Not: REM |
| Question 3: differences in sample size |
| Are there strong differences in sample size (more than 5:1) in the studies? |
| Yes: Consider that the REM increases the influence of small studies, more prone to publication bias; it may be better the FEM |
| Not: REM |
| Question 4: number of the to be combined |
| How many studies are to be pooled? |
| <20: REM if question 3 is answered negatively |
| ≥20: To take into account the previous questions before election |
| Question 5: sample size of most primary studies |
| It is very high, e.g., >5000 participants? |
| Yes: Consider REM, as any minor difference in effect estimates would be highly significant with FEM |
| No: To take into account the previous questions before election |
| Question 6: heterogeneity |
| Is there heterogeneity in pooled effect estimate? |
| Yes: If it is not explained by additional analyses (see the text), the pooled estimate has no sense |
| No: FEM |
| Question 7: publication bias |
| Is there publication bias? |
| Yes: If it is possible, give stratified analyses by sample size (either with the FEM or REM), assessing heterogeneity, and offer a tentative explanation for the differences |
| No: See the other questions |
Finally, there are validated guidelines to evaluate a systematic review.13,15 The protocol AMSTAR is detailed in Table 6.15 In the PRISMA statement the preferred reporting items for systematic reviews and meta-analysis are detailed.60 Remember that the quality of the inference obtained by a meta-analysis is not better that the quality of the primary studies: if one meta-analyzes garbage the product will be meta-analyzed garbage, just garbage.
The AMSTAR scale for evaluating systematic reviews.15
| Item | Question |
|---|---|
| 1 | Was an “a priori” design provided? |
| 2 | Was there duplicate study selection and data extraction? |
| 3 | Was a comprehensive literature search performed? |
| 4 | Was the status of publication (i.e., grey literature) used as an inclusion criterion? |
| 5 | Was a list of studies (included and excluded) provided? |
| 6 | Were the characteristics of the included studies provided? |
| 7 | Was the scientific quality of the included studies assessed and documented? |
| 8 | Was the scientific quality of the included studies used appropriately in formulating conclusions? |
| 9 | Were the methods used to combine the findings of studies appropriate? |
| 10 | Was the likelihood of publication bias assessed? |
| 11 | Were potential conflicts of interest included? |
The authors declare no conflict of interests.