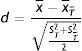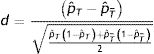Random allocation of treatment or intervention is the key feature of clinical trials and divides patients into treatment groups that are approximately balanced for baseline, and therefore comparable covariates except for the variable treatment of the study. However, in observational studies, where treatment allocation is not random, patients in the treatment and control groups often differ in covariates that are related to intervention variables. These imbalances in covariates can lead to biased estimates of the treatment effect. However, randomized clinical trials are sometimes not feasible for ethical, logistical, economic or other reasons. To resolve these situations, interest in the field of clinical research has grown in designing studies that are most similar to randomized experiments using observational (i.e. non-random) data. Observational studies using propensity score analysis methods have been increasing in the scientific papers of Intensive Care. Propensity score analyses attempt to control for confounding in non-experimental studies by adjusting for the likelihood that a given patient is exposed. However, studies with propensity indexes may be confusing, and intensivists are not familiar with this methodology and may not fully understand the importance of this technique. The objectives of this review are: to describe the fundamentals of propensity index methods; to present the techniques to adequately evaluate propensity index models; to discuss the advantages and disadvantages of these techniques.
Una de las características fundamentales de los ensayos clínicos es la asignación aleatoria de un tratamiento o intervención sobre los pacientes. Esta asignación divide los pacientes en dos grupos que, aunque difieran por el tratamiento recibido, presentan unas características basales homogéneas haciendo que ambos grupos sean comparables y se pueda evaluar el efecto causal del tratamiento. Por otro lado, los estudios observacionales se caracterizan por la asignación no aleatoria del tratamiento y por lo tanto que los grupos de pacientes no solo difieran por el tratamiento recibido, sino también por otras características basales, a menudo relacionadas con la variable de intervención. En numerosas ocasiones, los ensayos clínicos aleatorizados no son factibles por razones éticas, logísticas, económicas o de otro tipo. Uno de los retos de la investigación clínica en Cuidados Intensivos debería ser aprovechar los datos que provienen de la práctica clínica habitual y analizarlos como si fueran ensayos clínicos. Los estudios observacionales utilizando métodos de análisis con índices de propensión (propensity score) han ido en aumento en los artículos científicos de Cuidados Intensivos. Los análisis de índices de propensión intentan controlar la confusión en estudios observacionales ajustando la probabilidad de que un determinado paciente esté expuesto. Sin embargo, los estudios con índices de propensión pueden ser confusos, y los intensivistas no están familiarizados con esta metodología y pueden no comprender plenamente la importancia de esta técnica. Los objetivos de esta revisión son: describir los fundamentos de los métodos del índice de propensión; presentar las técnicas para evaluar adecuadamente los modelos de índices de propensión, y discutir las ventajas y los inconvenientes de estas técnicas.
In clinical research carried out in Intensive Care Units (ICUs), one of the common objectives is to evaluate the causal relationship between a given treatment or intervention (exposure) and the health outcome of a patient (death, healing, discharge from the ICU). Clinical trials are the reference research design when assessing the efficacy of a treatment in relation to the event of interest, since they reduce the risk of confounding influences or selection bias. Clinical trials involve the random assignment or allotment of a series of patients with a similar disease stage in order to assess the impact of such treatment upon the outcome. In the ICU setting, this outcome is usually defined as mortality during admission to the Unit or during the first 28 days after admission, or as the need for more aggressive treatment (e.g., tracheotomy).1–3
Assignment to treatment is the principal characteristic of clinical trials. The type of treatment for each patient is determined on a random basis in order to ensure that both the treated and the untreated patients present homogeneous features, thereby preventing the effect of the treatment from being confounded by the characteristics of the patients.
Although clinical trials are considered to be the highest quality studies for estimating causality, they also have some limitations: the sample size is typically of limited size and difficult to achieve; external validity is low; the application of inclusion criteria narrows down the population analyzed (since elderly patients, individuals with comorbidities or pregnant women tend to be excluded); ethical issues must be taken into account; and the duration of follow-up is limited.4
In the case of the ICU there are additional factors that make the designing of clinical trials in this setting particularly difficult, such as nosographic shortcomings (patients admitted to the ICU present syndromes such as for example acute respiratory distress syndrome [ARDS] instead of diseases); problems in defining adequate control groups; the concomitant use of different treatments (in many cases the intervention is not a drug but a therapeutic approach); randomization prior to treatment; or the obtainment of informed consent (which poses problems due to the moment in which consent is required).5
A possible solution to some of the difficulties of clinical trials is the conduction of observational studies. These represent a type of research in which treatment selection is conditioned to the baseline characteristics of the patient. The supervising physician decides the type of treatment according to the patient features. This is one of the main differences between observational studies and clinical trials.6–9
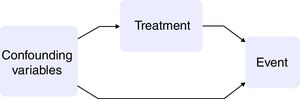
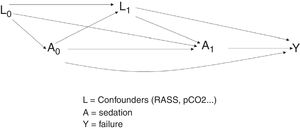
Observational studies have a number of advantages with respect to clinical trials: the population setting is broader; the duration of follow-up is longer; and the sample size is greater. In contrast, the fact that treatment allocation is not randomized implies that the estimation of causality is biased, and that the treated patients and untreated patients therefore differ not only in the treatment received but also in their baseline characteristics. If these baseline variables were associated to the event of interest, they would act as confounders between exposure and outcome10,11 (Fig. 1).
Statistical techniques are continuously developing, and new methods are increasingly used in clinical research to estimate causality in observational studies, considering the possible confounding factors – specifically the propensity score (PS) and marginal structural models.
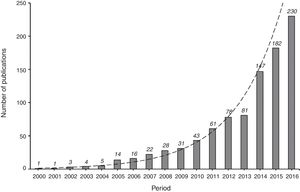
Articles using PS methods have become increasingly common in the Intensive Care literature over the last 10 years (Fig. 2). Since PS methodology is still not very familiar to intensivists, the present study establishes the underlying concept and describes the best practice for applying the method. Specifically, the aims of our study are to describe: (1) the principles of PS methods; (2) the main methods for using the propensity score (matching, stratification, covariate adjustment, and inverse probability of treatment weighting [IPTW]) in an Intensive Care example; (3) statistical analysis in the presence of time dependent confounders; and (4) the strong and weak points of these techniques.
The propensity score in observational studiesAccording to Rosenbaum and Rubin,12 the PS allows us to estimate the probability of assignment to a treatment, conditioned to the baseline characteristics of the patient. This is a balanced score, since treated patients and untreated patients with similar PS will have equivalent baseline characteristics. In this way we would control the confounding effect produced by the baseline characteristics.
Two conditions must be met in order to apply the PS: there must be no unmeasured confounding factors, and each subject must have a probability different from zero of receiving a treatment. If these two conditions are met, treatment allocation can be regarded as independent with respect to the results, when conditioning for the covariables.
In clinical trials the PS is known, since the probability of patient assignment to a given treatment is known (e.g., in the case of a study with two treatment arms, the probability of assignment of a patient to either arm will be 0.5). However, in observational studies this score is not known. It could be estimated through logistic regression, where the dependent variable is the treatment and the independent variables are the possibly confounding baseline covariables.
Variables to be considered in calculating the propensity scoreThe variables included in the PS can generate bias, modifying the variance of the estimator or error, if not correctly chosen. There is no consensus regarding the choice of such variables, since this depends on the clinical approach – defining the variables based on clinical criterion – and the statistical approach used.13
A given set of baseline variables can be classified into: (1) variables related to the event; (2) variables related to the exposure; and (3) variables related to both the event and to the exposure.
As we are dealing with a logistic regression model, the number of variables is determined by the total number of exposed/unexposed patients, following the rule of Peduzzi, i.e., 10 patients per event of interest (exposed/unexposed).
Simulation studies have shown that the variables related to the result (event) must be included, along with the variables showing an association to the event and to the exposure.14 Variables only showing an association to the treatment are not to be included.
The choice of variables is a challenge in which balanced agreement between statistical findings and clinical criterion must be established.
Propensity score application methodsOnce the PS has been estimated for all the patients, different application methods can be used: matching, stratification, IPTW, and adjustment of the final model, including it as a confounding covariable.
MatchingMatching is based on creating a new patient sample according to the previously estimated PS. Patients with similar PS are selected to create pairs of treated patients and untreated patients. The aim of this method is to create a new balanced sample and reduce the differences there may be between patients in the two groups. Matching allows the generation of pairs considering different aspects. In this regard, replacement could be considered, and therefore it could be decided whether an individual can be matched twice. The patient may be matched to the “neighboring” patient that is closer. Likewise, a caliper may be established, indicating the maximum separating distance with which two patients can be matched – the value usually being 0.25 times the standard deviation of the PS.
With this new sample, presenting a structure very similar to that of a clinical trial, we could solve the confounding problem and would be reducing the differences in the characteristics of the treated patients and controls.
In the matched sample, and based on standardized differences, we would have to check that the difference in baseline characteristics of the treated patients and the untreated patients after matching is less than 10%.15
The standardized differences are expressed as follows for continuous variables:
where x¯T, x¯T¯ are the means of the variables in the treated and untreated patients, respectively, and ST2, ST¯2 are the variances of those variables.Likewise, we define the standardized differences for dichotomic variables:
where pˆT is the proportion of events of a variable for the treated individuals, and pˆT¯ is the proportion for untreated individuals.The last step is to estimate the effect of the treatment upon the event of interest in the matched sample. If the response variable is continuous, we can estimate the difference between the two groups by means of the Student t-test or the Wilcoxon test in the absence of a normal distribution. If the response variable is dichotomic, the effect is estimated using the McNemar test.
Inverse probability treatment weighting (IPTW)This method involves weighting estimates based on the PS, calculated as the inverse of the probability for treated and untreated patients, followed by estimation of the effect of the treatment weighted for the previously calculated weight.
StratificationThe stratification method consists of dividing the sample into several subsamples based on the PS. The number of groups is usually 5, according to quintiles or other percentiles of the estimated PS. Rosenbaum et al. indicate that bias can be lowered 90%. The effect of the treatment is estimated based on the Mantel-Haenszel (MH) odds ratio (OR).
Propensity scoreThe last alternative is to calculate the effect of the treatment entering the PS as covariable in the model. This method is based on the premise that the relationship between the outcome (event) and the confounding variable must be correctly specified, i.e., that it has been established correctly; the use of nonlinear models, splines or fractional polynomials could help to establish adequate models.
Comparison of the different methodsThe advantage of the matching method is that once the pairs have been obtained, the new structure is similar to that of a clinical trial. In contrast, this technique requires a large sample in which there are more untreated patients than treated patients, in order to ensure that all treated patients can be matched. By matching we moreover would lose all the information corresponding to those patients that could not be matched.
The main advantage of the stratification method is that we can use the entire patient sample. Furthermore, it is a more robust technique in the event the PS has not been correctly specified in comparison with the IPTW method or covariable.
According to Deb et al.,15 a disadvantage of the IPTW method is that the calculated weights may be unstable if there are patients with low probabilities of receiving treatment: if the weight is regarded as the inverse of the PS, those patients with a low PS will be assigned a greater weight than those with a high PS.
Considering PS as covariable of the model, we obtain a simple way to include many variables in the latter. In order to use this method, it must be checked that the relationship between PS and the outcome has been correctly specified; the assumption of a normal distribution should be confirmed if the regression model is linear. The inconvenience here is that checking the balance of the baseline variables (diagnostic balance) is more complicated than in other methods, and it has been demonstrated that more biased estimates are obtained.15 Lastly, implementation of this method does not allow the estimation of absolute risk reduction or of the number needed to treat (NNT).
Propensity score and regressionUnder certain conditions, the estimated obtained by the multivariate regression models and PS are coincident. The difference between PS and logistic regression is strongly conditioned to the number of events and to the number of covariables to adjust for.16
According to Harrell et al.,17 the optimum number of independent variables that should be entered in a logistic regression model is 10 times the number of events in the sample—a condition known as the “rule of 10”. In other words, if the number of events is 30 (deaths, for example), the optimum number of explanatory variables for estimating the probability of death would be three. Logistic regression therefore will depend on the number of events and consequently on the sample size.18
However, in the logistic regression of PS, the dependent variable is not the event but exposure. The number of variables for estimating exposure will depend not only on their association to the event as commented above, but also on the number of exposures there are. If for example the number of exposures is 60 (60 smokers), we should adjust PS with 6 variables.
Depending on the prevalence of the event and on the number of subjects exposed to the treatment, PS allows us to fit a model with more variables than the logistic regression model.
Time dependent confounders. Marginal structural modelsThe PS is a statistical technique that allows us to estimate the effect of the treatment upon the patient outcome. When the clinical confounding variables are time dependent, estimation of the score is more complex, since the values of the confounding variables vary over time.
Example. In evaluating the causal relationship between sedation (A) and the failure of noninvasive mechanical ventilation (Y), we may encounter confounding variables (L) such as for example the RASS sedation scale or certain respiratory markers such as pH or PaCO2.18,19
Both the RASS sedation scale and the respiratory markers (pH or PaCO2) are measured in different time intervals. They therefore are regarded as time dependent confounding parameters if the weighted values of the covariables can predict current treatment or if the current values can predict future results, conditioned to the treatment received in the past.
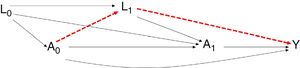
In this example, and as can be seen in Fig. 3, we seek to estimate the effect of treatment in the form of sedation (A) in both instant 0 (A0) and in instant 1 (A1). On the other hand, L1 represents the confounding variables (RASS score and pCO2) measured in instant 1, and Y represents the outcome of interest (failure of noninvasive ventilation). On studying the relationship between the treatment in instant 0 and the outcome, two causal routes appear: A0–Y and A0–L1–Y. Route A0–Y is a direct route.
However, in route A0–L1–Y, the relationship established between the treatment and the outcome is conditioned to the confounding variables L1. To estimate the effect, according to the classical models, we could resort to regression without considering the confounders L1, since they are found in the same causal chain between the effect (A0) and the outcome (Y) (Fig. 4).
Representative diagram of the time dependent confounding variables in the observational studies. The possibility exists that a relationship could be established between the exposure variable and outcome simply influenced by the presence of the time dependent confounding variables (alternative route in red), and not really by the existence of a causal relationship between exposure and outcome.
If we estimate the effect without adjusting for L1, bias would be produced, since we would not be taking into account the causal route between A1 and Y which is conditioned by L1. The regression methods can pose problems of bias even in the absence of residual confounding elements. This is possibly due to the confusion created by the time dependent variables in assignment of the previous treatment.
There are a number of alternatives for estimating the effect of a treatment in the presence of time dependent confounders: marginal structural models and nested structural models.20
Marginal structural models19 are considered an alternative to regression models when there is a time dependent confounding variable associated to the outcome of interest and which is also related to the treatment being evaluated. The term “structural” indicates a causal effect, not only a statistical association.
Instead of combined distributions, use is made of marginal distributions conditioned to the baseline variables: the term “marginal models” is therefore used.
Estimation of effect based on a marginal structural modelIn creating the marginal structural models, the first step is to estimate PS based on logistic regression or probit models, in which the dependent variable is the treatment and the independent variables are those parameters associated with the start of treatment and/or with the event of interest.
Each patient contributes as many observations as number of time units followed (months, weeks, etc.). The variable follow-up time is to be added as covariable.
The weight of each patient and time is estimated according to the probabilities predicted by this model, based on the inverse of the probability of treatment actually received. In this context, it is assumed that there are no competing events, since each patient is considered to be followed-up on until the event of interest occurs, or the patient is lost to follow-up.
In the same way as above, a weight is estimated for each patient, for censoring.
Based on their product, we combine the weights obtained of the treatment and of the probability of censoring. With such weighting, we can simulate a sample in which treatment and censoring are independent of the measured confounders. In the event of very small probabilities, the outlier weightings are replaced by near lying percentiles21 (1 and 99 or 2.5 and 97.5), thereby avoiding the presence of very large weighting values.
If the event of interest is a binary variable, the OR of the logistic regression between the event and treatment, weighted for the combined weight, offers a good approximation to the instantaneous relative risk of the Cox model, because the risk of events is low in all the months.
AssumptionsIn order to use the above described statistical methods we need to check certain assumptions:
- •
The time order: exposure to treatment occurs before the event.
- •
Consistency: the potential result of an individual, conditioned to the observed treatment history, coincides with the true result observed.
- •
Positivity: the individuals of the population must show a probability of over zero of receiving the treatment in each treatment category and in each of the levels of the confounding variables. In this way, the mean causal effect of the treatment can be estimated within each subgroup of the population established by the confounding variables.
- •
Correct specification of the model: the model has been estimated adequately. The assumption of linearity is to be evaluated.
- •
Absence of residual confusion: this can be checked by means of a sensitivity analysis, since it cannot be assumed using only the data of the patients.
The fundamental advantage of the PS is that it summarizes the baseline characteristics of the investigated individuals in a single number. The score summarizes the probability of exposure with a number.
For example, if the objective of the study is to evaluate the effect of noninvasive ventilation in children admitted to the ICU in an observational study of over 30,000 patients of which almost one-third receive noninvasive ventilation as first option, this type of research question could have been addressed—with difficulties—by means of a clinical trial.22
This type of analysis has also been used to estimate the adjusted effect of cancer upon mortality in the ICU,23 since this investigation can only be addressed in clinical research by means of observational studies.
We could also use these analytical techniques to estimate the effect of a complication such as weakness acquired in the ICU (WICU) upon weaning failure or patient mortality during admission to the ICU.24,25
We will develop this latter example step by step. The study involved is a prospective, international multicenter trial involving 4157 patients subjected to mechanical ventilation during more than 12h. The appearance of WICU during admission was associated to an increased incidence of weaning failure and to higher mortality in the ICU. The PS was estimated with the following variables: age, SAPS II score upon admission to the ICU, main reason for starting mechanical ventilation (chronic obstructive pulmonary disease, heart failure, sepsis, acute respiratory distress syndrome and pneumonia).
In order to evaluate the impact of sedation and analgesia in patients subjected to noninvasive ventilation upon the need for endotracheal intubation, and in the presence of time dependent confounders such as the RASS (Richmond Agitation-Sedation Scale) or PCO2, we must consider a marginal structural model. To illustrate the use of these methods comparing the different PS options, and exhibiting the results based on classical methods such as logistic regression, we will use a series of data from a multicenter study in the ICU involving mechanical ventilation.
First partConsidering as treatment the interruption of sedation and as event the death of the patient, PS has been applied to assess causality. On applying different PS modalities (matching, stratification, IPTW, and as covariable of the model) for this clinical scenario, we obtained similar estimates in terms of OR and 95% confidence intervals (95%CI). These ORs have been compared with those obtained estimating the effect without PS (Table 1).
Relationship between mortality risk on day 28 (status day 28) and the interruption of sedation, according to different propensity analytical strategies.
| Applications of the propensity score | Without propensity score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Matching | IPTW | Stratification MH | Covariable | LR univariate | LR multivariate | |||||||
| OR | 95%CI | OR | 95%CI | OR | 95%CI | OR | 95%CI | OR | 95%CI | OR | 95%CI | |
| Status day 28 | 0.64 | (0.49; 0.83) | 0.67 | (0.52; 0.85) | 0.68 | (0.53; 0.86) | 0.67 | (0.52; 0.85) | 0.64 | (0.52; 0.80) | 0.63 | (0.49; 0.81) |
CI: confidence interval; IPTW: inverse probability of treatment weighting; MH: Mantel-Haenszel; OR: odds ratio; LR: logistic regression.
These such comparable results are attributable to the fact that in relation to the baseline characteristics, the treated and untreated patients do not differ, and the estimated PS is therefore very similar in both sets of individuals.
Second partIf we consider a series of patients with more different baseline characteristics, the obtained estimates of the effect of treatment would not be consistent among the different methods. For example, if we only consider those patients with respiratory disease and wish to study the effect of neuromuscular blockers upon patient delirium, the different methods would yield different estimates (Table 2).
Relationship between mortality risk on day 28 (status day 28) and the interruption of sedation, according to different propensity analytical strategies.
| Applications of the propensity score | Without propensity score | ||||
|---|---|---|---|---|---|
| OR | 95%CI | OR | 95%CI | ||
| Matching | 1.72 | (0.55; 5.97) | Univariate | 2.79 | (1.26; 6.17) |
| IPTW | 2.08 | (0.83; 5.24) | Multivariate | 3.18 | (1.42; 7.13) |
| Stratification | 1.81 | (1.14; 7.14) | |||
| Covariable | 2.06 | (0.84; 5.11) | |||
CI: confidence interval; IPTW: inverse probability of treatment weighting; OR: odds ratio.
The weightings obtained from IPTW span the following values: [1.037; 12.75].
When treated and untreated patients differ, and the number of events and exposures is small, the statistical methods show significant differences.
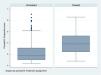
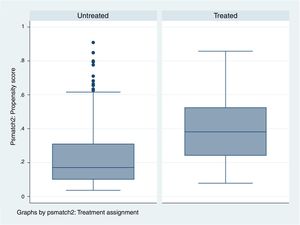
In order to see how the treated and untreated patients are distributed based on the estimated PS, we examine the zone of common support, i.e., the range of common values which PS presents in both groups.
Therefore, the more similar the treated and untreated patient groups, the larger the number of patients of both groups included in the zone of common support.
If the treated and untreated patients are very similar, the zone of common support includes all the individuals, since the maximum and minimum of both PS will be similar. In contrast, if both groups are very different, the most likely result is that the number of patients entering the zone of common support will be smaller (Fig. 5 and Table 3).
Comparison of the standardized differences of the baseline variables in treated and untreated patients, before and after matching, to confirm that the propensity score (PS) is correctly specified. If these differences exceed 10%, PS has not been adequately calculated.
| Before matching | After matching | |||||
|---|---|---|---|---|---|---|
| NMB=yes (n=148) | NMB=no (n=390) | Standardized differences (%) | NMB=yes (n=141) | NMB=no (n=381) | Standardized differences (%) | |
| Baseline variables | ||||||
| Age (years) mean (SD) | 59.53 (13.53) | 65.33 (13.58) | 42.79 | 60.53 (14.53) | 58.96 (13.64) | 11.17 |
| SAPS_II (points), mean (SD) | 43.74 (15.49) | 46.83 (16.76) | 19.15 | 44.99 (15.67) | 43.41 (14.78) | 10.37 |
| Gender (M) | 56.8 | 48.5 | 16.63 | 55 | 58.3 | 6.73 |
| Invasive ventilatory support (yes) | 21.6 | 21.3 | 0.59 | 23.3 | 21.7 | 3.98 |
| Presence of cardiovascular failure (Yes) | 68.9 | 40.8 | 58.37 | 67.5 | 68.3 | 1.78 |
| Presence of renal failure (yes) | 42.6 | 21.28 | 40.87 | 36.7 | 40 | 6.85 |
| Presence of Hematological failure (yes) | 24.3 | 8.97 | 25.75 | 19.2 | 16.7 | 6.52 |
| Sepsis during mechanical ventilation | 43.24 | 24.1 | 37 | 40.88 | 45.83 | 10.10 |
| Duration of ventilatory support (days) | 15.90±13.14 | 8.21±14.82 | 54.91 | 14.35±11.60 | 11.97±19.04 | 15.09 |
In order to establish whether the order of the subjects in the matching method exerts an influence, we simulated 100 models and obtained the corresponding OR estimates. We see that when the number of variables for which PS is adjusted is high, the order of matching exerts no influence, and similar estimates are obtained. When the number of variables for which the order of matching is adjusted does exert an influence, different estimates are obtained.
Advantages and inconveniences of these techniquesDepending on the number of events and exposures involved, it has been seen that PS and logistic regression could be regarded as equivalent, yielding similar estimates when no differences are observed between treated and untreated patients, and the number of events is high.
When the number of events is low, PS allows adjustment for more variables than logistic regression, and moreover quantifies the effect of treatment.
Matching of the PS results in a structure similar to that of a clinical trial (the pairs show similar characteristics), with the disadvantage that those patients not matched are excluded from the study.
Because of the random patient allotment involved, randomized clinical trials have the advantage of being able to assess the causal relationship directly. When such studies are not viable, however, observational studies can be regarded as an alternative. In order to assess causality in observational studies, we first must solve the confounding problems they imply.
ConclusionsClinical trials represent the best methodological design for analyzing causality in clinical research. However, certain hypotheses cannot be tested clinically due to ethical, methodological or economical limitations. In order to overcome such limitations, observational studies are able to simulate the hypothetical scenario of a clinical trial, using PS and marginal structural models to provide the desired answers. The growing interest in this new methodology makes it necessary to familiarize intensivists with it in order to facilitate its application to clinical research in the Intensive Care setting.
As an example, Delaney et al.21 described the use of the statistical methods detailed in this article to evaluate the effect of corticosteroids upon mortality among patients with influenza A (H1N1pdm09). The ORs associated to these models ranged from 1.85 (95%CI: 1.12–3.04) in the classical multivariate logistic regression models to 1.71 (95%CI: 1.05–2.78) in the logistic regression model adjusted for PS, 1.52 (95%CI: 0.90–2.58) after matching of the PS, and 0.96 (95%CI: 0.28–3.28) in the marginal structural model adjusting for the time dependent variables. On adjusting for the time dependent variables in the marginal structural model, no association was observed between corticosteroid use and patient mortality.
Conflict of interestThe authors declare that they have no conflicts of interest (economical, commercial or intellectual) in relation to this study.
Please cite this article as: Coscia Requena C, Muriel A, Peñuelas O. Análisis de la causalidad desde los estudios observacionales y su aplicación en la investigación clínica en Cuidados Intensivos. Med Intensiva. 2018;42:292–300.