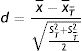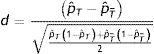Una de las características fundamentales de los ensayos clínicos es la asignación aleatoria de un tratamiento o intervención sobre los pacientes. Esta asignación divide los pacientes en dos grupos que, aunque difieran por el tratamiento recibido, presentan unas características basales homogéneas haciendo que ambos grupos sean comparables y se pueda evaluar el efecto causal del tratamiento. Por otro lado, los estudios observacionales se caracterizan por la asignación no aleatoria del tratamiento y por lo tanto que los grupos de pacientes no solo difieran por el tratamiento recibido, sino también por otras características basales, a menudo relacionadas con la variable de intervención. En numerosas ocasiones, los ensayos clínicos aleatorizados no son factibles por razones éticas, logísticas, económicas o de otro tipo. Uno de los retos de la investigación clínica en Cuidados Intensivos debería ser aprovechar los datos que provienen de la práctica clínica habitual y analizarlos como si fueran ensayos clínicos. Los estudios observacionales utilizando métodos de análisis con índices de propensión (propensity score) han ido en aumento en los artículos científicos de Cuidados Intensivos. Los análisis de índices de propensión intentan controlar la confusión en estudios observacionales ajustando la probabilidad de que un determinado paciente esté expuesto. Sin embargo, los estudios con índices de propensión pueden ser confusos, y los intensivistas no están familiarizados con esta metodología y pueden no comprender plenamente la importancia de esta técnica. Los objetivos de esta revisión son: describir los fundamentos de los métodos del índice de propensión; presentar las técnicas para evaluar adecuadamente los modelos de índices de propensión, y discutir las ventajas y los inconvenientes de estas técnicas.
Random allocation of treatment or intervention is the key feature of clinical trials and divides patients into treatment groups that are approximately balanced for baseline, and therefore comparable covariates except for the variable treatment of the study. However, in observational studies, where treatment allocation is not random, patients in the treatment and control groups often differ in covariates that are related to intervention variables. These imbalances in covariates can lead to biased estimates of the treatment effect. However, randomized clinical trials are sometimes not feasible for ethical, logistical, economic or other reasons. To resolve these situations, interest in the field of clinical research has grown in designing studies that are most similar to randomized experiments using observational (i.e. non-random) data. Observational studies using propensity score analysis methods have been increasing in the scientific papers of Intensive Care. Propensity score analyses attempt to control for confounding in non-experimental studies by adjusting for the likelihood that a given patient is exposed. However, studies with propensity indexes may be confusing, and intensivists are not familiar with this methodology and may not fully understand the importance of this technique. The objectives of this review are: to describe the fundamentals of propensity index methods; to present the techniques to adequately evaluate propensity index models; to discuss the advantages and disadvantages of these techniques.
En la investigación clínica desarrollada en las Unidades de Cuidados Intensivos (UCI), uno de los objetivos habituales es evaluar la asociación causal que existe entre un tratamiento o intervención (exposición) y el desenlace de salud de un paciente (muerte curación, alta en UCI). Los ensayos clínicos representan el diseño de investigación de referencia cuando se quiere evaluar la eficacia que produce el tratamiento sobre el evento de interés, ya que se reduce la probabilidad de aparición de sesgos de selección o confusión. Los ensayos clínicos consisten en asignar un tratamiento aleatoriamente a un conjunto de pacientes con un estadio de la enfermedad similar para estimar el efecto que este presente sobre el desenlace; habitualmente en UCI este desenlace es mortalidad durante la estancia en UCI, o durante los 28 días tras su ingreso, o la necesidad de realizar un tratamiento más agresivo, como por ejemplo la traqueotomía1-3.
La asignación del tratamiento es la característica principal de los ensayos clínicos. La elección del tratamiento de cada paciente se realiza de forma aleatoria para que pacientes tratados y no tratados presenten características homogéneas y en consecuencia el efecto del tratamiento no se vea confundido por las características de los pacientes.
Aunque se consideren los estudios de más calidad, para la estimación de la causalidad, los ensayos clínicos también presentan algunas limitaciones: el tamaño muestral es reducido y difícilmente alcanzable, cuentan con una baja validez externa, los criterios de inclusión reducen el marco de la población a analizar, ya que tienden a excluir pacientes con edades avanzadas y con más de una enfermedad, mujeres; además, los ensayos clínicos presentan aspectos éticos a tener en cuenta y el tiempo de seguimiento es reducido4.
En el caso de la UCI, existen además otras dificultades que hacen que el diseño de ensayos clínicos en nuestra disciplina sea particularmente difícil, como son: falta de nosografía segura —los pacientes ingresados en UCI presentan síndromes (por ejemplo, síndrome de distrés respiratorio agudo [SDRA]) en vez de enfermedades—, dificultades para identificar grupos control adecuados, el uso concomitante de diferentes terapias (a menudo la intervención no es un medicamento sino una actitud terapéutica), la aleatorización antes del tratamiento y la solicitud de consentimiento informado es difícil debido al momento en que se produce5.
Una posible solución a algunas de las dificultades de los ensayos clínicos son los estudios observacionales. Son un tipo de investigación cuya selección del tratamiento está condicionada a las características basales del paciente. El propio médico determina el tipo de tratamiento en función de las características que presenta el paciente. Esta es una de las principales diferencias entre ambos estudios6-9.
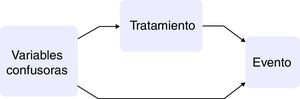
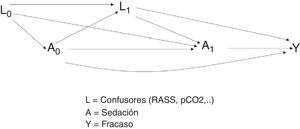
Los estudios observacionales presentan varias ventajas en comparación con los ensayos clínicos: el marco de la población es más amplio, así como el tiempo de seguimiento, y presentan un tamaño muestral mayor. Por otra parte, el hecho de que la asignación del tratamiento no sea aleatoria conlleva que la estimación de la causalidad sea sesgada y, en consecuencia, que pacientes tratados y no tratados difieran no solo en el tratamiento que reciben sino también en las características basales. Si estas variables basales tuvieran asociación con el evento de interés, se estaría indicando que son variables confusoras entre la exposición y el desenlace10,11 (fig. 1).
Las técnicas estadísticas están en continuo desarrollo y se han ido incorporando nuevos métodos cada vez más utilizados en la investigación clínica que permiten estimar la causalidad en estudios observacionales teniendo en cuenta los posibles factores de confusión, concretamente el índice de propensión (IP) (propensity score) y los modelos marginales estructurales (marginal structural models).
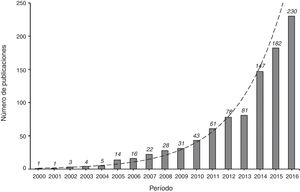
Los artículos publicados utilizando los métodos de IP han ido incrementándose cada vez más en la literatura científica de Cuidados Intensivos en los últimos 10 años (fig. 2). Dado que la metodología de los IP no es aún muy familiar para los intensivistas, en este artículo se presenta el marco conceptual en que se basan y se indican las mejores prácticas para su aplicación. Por tanto, los objetivos de esta revisión son describir: 1) los fundamentos de los métodos del IP; 2) los métodos principales para el uso de la puntuación de la propensión (emparejamiento, estratificación, ajuste por covariable y ponderación por el inverso de la probabilidad de tratamiento (inverse probability of treatment weighting [IPTW]) en un ejemplo de Cuidados Intensivos; 3) el análisis estadístico ante la presencia de confusores tiempodependientes, y 4) los puntos fuertes y débiles de estas técnicas.
El índice de propensión en los estudios observacionalesEl IP, según Rosenbaum y Rubin12, es un método que permite estimar la probabilidad de asignación a un tratamiento condicionada a las características basales que el paciente presente. Este índice es balanceado, puesto que pacientes tratados y no tratados con IP similares tendrán características basales equivalentes. De este modo se estaría controlando el efecto de la confusión producido por las características basales.
Para que se pueda aplicar el IP, se deben cumplir dos condiciones: que no haya factores de confusión no medidos y, además, que cada sujeto presente una probabilidad distinta de cero de recibir un tratamiento. Si se cumplen estas dos condiciones, se puede decir que la asignación del tratamiento es independiente con respecto al resultado, cuando se está condicionando por las covariables.
En los ensayos clínicos el IP es conocido, puesto que se conoce con qué probabilidad se asigna un tratamiento a un paciente (por ejemplo, si es un estudio con dos ramas de tratamiento, la probabilidad de asignación de un sujeto será 0,5 respectivamente). Sin embargo, en los estudios observacionales este índice es desconocido. Se podría estimar mediante regresión logística: en el que la variable dependiente es el tratamiento y las variables independientes son las covariables basales posiblemente confusoras.
Variables a considerar en el cálculo del índice de propensiónLas variables incluidas en el IP pueden crear sesgos, modificando la varianza del estimador o el error si no están correctamente elegidas. Para seleccionar dichas variables no existe un consenso, ya que depende del planteamiento clínico, estableciendo las variables con criterio clínico, y del planteamiento estadístico13.
Dado un conjunto de variables basales, se pueden clasificar en 1) variables que se relacionan con el evento, 2) variables que se relacionan con la exposición y 3) variables que se asocian tanto con el evento como con la exposición.
Al ser un modelo de regresión logística, el número de variables viene determinado por el número total de expuestos/no expuestos siguiendo la regla de Peduzzi, es decir, 10 pacientes por evento de interés (expuesto/no expuesto).
En estudios de simulación se ha podido comprobar que las variables que se relacionan con el resultado (evento) se deben incluir, así como las variables que presenten asociación con el evento y la exposición14. No se deberán incluir aquellas variables que presenten asociación solo con el tratamiento.
La elección de las variables constituye un reto en el que se deben consensuar hallazgos estadísticos y criterio clínico.
Métodos de aplicación de los índices de propensiónUna vez que el IP ha sido estimado para todos los pacientes, hay distintos métodos de aplicación: mediante emparejamiento (matching), estratificación, IPTW, y ajustando el modelo final incluyéndolo como covariable confusora.
EmparejamientoEl método del emparejamiento se basa en crear una nueva muestra de pacientes en función del IP estimado previamente. Se seleccionan los pacientes con IP similares para crear parejas de pacientes tratados y pacientes no tratados. El objetivo de este método es crear una nueva muestra balanceada y reducir las diferencias que pueda haber entre pacientes de ambos grupos. Este método permite realizar parejas considerando diversos aspectos: se podría tener en cuenta el reemplazamiento, por lo tanto, se podría decidir si un individuo puede encontrar pareja dos veces; se puede emparejar por el «vecino», paciente, que esté más cercano; y también se puede fijar un calibre (caliper) que indique la distancia máxima con la que se puede emparejar a dos pacientes, que suele ser el 0,25 por la desviación estándar del IP.
Con esta nueva muestra, con estructura muy similar a la de un ensayo clínico, se estaría solucionando el problema de la confusión y se estarían reduciendo las diferencias de las características de pacientes tratados y controles.
En la muestra emparejada, habría que comprobar, mediante diferencias estandarizadas, que las características basales de los pacientes tratados y los no tratados, después del emparejamiento, sean menores en un 10%15.
Las diferencias estandarizadas se expresan de la siguiente forma para las variables continuas:
Siendo x¯T,x¯T¯ las medias de las variables en los tratados y en los no tratados, y ST2,ST¯2 las varianzas de dichas variables.
Del mismo modo se definen las diferencias estandarizadas para variables dicotómicas:
Donde pˆT es la proporción de eventos de una variable para los individuos tratados y pˆT¯ es la proporción para individuos no tratados.
El último paso es realizar la estimación del efecto del tratamiento sobre el evento de interés en la muestra emparejada. Si la variable respuesta es continua se podrá estimar la diferencia entre los dos grupos mediante el test de la t de Student o, en caso de no cumplir con la hipótesis de normalidad, mediante el test de Wilcoxon. Si la variable respuesta es dicotómica, se estimará el efecto mediante el test de McNemar.
Inverse probability treatment weighting (IPTW)Consiste en estimar pesos basados en el IP, calculados como la inversa de dicha probabilidad para tratados y no tratados, y posteriormente realizar la estimación del efecto del tratamiento ponderando por el peso anteriormente calculado.
EstratificaciónEl método de estratificación consiste en dividir la muestra en varias submuestras basadas en el IP. El número de grupos a utilizar suele ser 5, en función de los quintiles o de otros percentiles del IP estimado. Rosenbaum et al. indican que se consigue reducir el sesgo en un 90%. El efecto del tratamiento se estimará mediante la odds ratio (OR) de Mantel-Haenszel (MH).
Índice de propensiónLa última alternativa consiste en calcular el efecto del tratamiento incluyendo el IP como covariable del modelo. Este método tiene la premisa de que la relación entre el desenlace (evento) y la variable confusora debe estar correctamente especificada. Es decir, que se haya realizado de forma correcta; el empleo de métodos no lineales, splines o polinomios fraccionales podría ayudar a establecer modelos adecuados.
Comparación entre los distintos métodosEl método del emparejamiento presenta la ventaja de que, una vez que se han obtenido las parejas, la nueva estructura se asemeja a la de un ensayo clínico. Por otro lado, esta técnica necesita una muestra grande donde haya un mayor número de pacientes no tratados que tratados para que todos los pacientes tratados puedan encontrar pareja. Al emparejar, además, se estaría perdiendo toda la información de aquellos pacientes que no encontraron pareja.
La ventaja principal que presenta el método de estratificación es que permite utilizar toda la muestra de los pacientes. Además, es una técnica más robusta si el IP no está correctamente especificado en comparación con el método del IPTW o el de la covariable.
El método IPTW, según Deb et al.15, tiene la desventaja de que los pesos calculados pueden ser inestables si hay pacientes con probabilidades bajas de recibir el tratamiento: si el peso se considera como la inversa del IP, aquellos pacientes con un IP bajo obtendrán un peso mayor que los pacientes con un IP alto.
Considerando el IP como covariable del modelo, se consigue de forma sencilla poder incluir un gran número de variables en el modelo. Para poder utilizar este método hay que comprobar que la relación entre el IP y el desenlace esté correctamente especificada; la asunción de normalidad debería ser comprobada si el modelo de regresión es lineal. Presenta el inconveniente de que la comprobación del balance de las variables basales (balance diagnóstico) es más complicada que en otros métodos, además de haberse demostrado que produce estimaciones más sesgadas15. Por último, la implementación que se tiene de este método no permite la estimación de la reducción absoluta del riesgo o del número necesario para tratar (NNT).
Índice de propensión y regresiónBajo ciertas condiciones, las estimaciones obtenidas por los modelos de regresión multivariables y el IP son coincidentes. La diferencia entre el IP y la regresión logística está muy condicionada al número de eventos y al número de covariables por las que ajustar16.
Según Harrell et al.17, el número óptimo de variables independientes que se debería incluir en un modelo de regresión logística es 10 veces el número de eventos que se tienen en la muestra, lo que se conoce como la regla del 10. Es decir, si el número de eventos es 30 (fallecimientos, por ejemplo), el número óptimo de variables explicativas para estimar la probabilidad de fallecer debería ser 3. La regresión logística dependerá por lo tanto del número de eventos y en consecuencia del tamaño muestral18.
Sin embargo, en la regresión logística del IP, la variable dependiente no es el evento, sino la exposición. El número de variables para estimar la exposición no solo dependerá de la asociación que presenten con el evento, como se decía anteriormente, sino también por el número de exposiciones que haya. Si, por ejemplo, el número de exposiciones fuera 60 (60 fumadores), se debería ajustar el IP con 6 variables.
Dependiendo de la prevalencia del evento y del número de expuestos al tratamiento, el IP permite ajustar un modelo con más variables que el modelo de regresión logística.
Confusores tiempodependientes. Modelos marginales estructuralesEl IP es una técnica estadística que permite estimar el efecto del tratamiento sobre el desenlace de un paciente. Cuando las variables clínicas confusoras son tiempodependientes, la estimación de dicho índice resulta más compleja puesto que los valores de las variables confusoras varían a lo largo del tiempo.
Ejemplo. Si se quisiera evaluar el efecto causal de la sedación (A) en el fracaso de la ventilación mecánica no invasiva (Y), podrían existir variables confusoras (L), por ejemplo, la escala de sedación de RASS o algunos marcadores respiratorios como el pH o la PaCO218,19.
Tanto la escala de sedación RASS como los marcadores respiratorios (pH o PaCO2) se miden en distintos periodos de tiempo. Por tanto, se considerarán como confusoras tiempodependientes si los valores pasados de la covariable pueden predecir el tratamiento actual o si los valores actuales podrán predecir resultados futuros, condicionados al tratamiento recibido en pasado.
En este ejemplo, según se observa en la figura 3, se quiere estimar el efecto del tratamiento de sedación (A), tanto en el instante 0 (A0) como en el instante 1 (A1). Por otro lado, L1 representa a las variables confusoras (escala RASS y pCO2) medidas en el instante 1, e Y representa el desenlace de interés (fracaso de la ventilación no invasiva). Al estudiar la relación entre el tratamiento en el instante 0 y el desenlace, aparecen dos caminos causales: A0–Y y A0–L1–Y. El camino A0–Y es un camino directo.
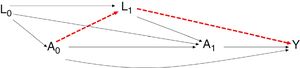
Sin embargo, en el camino A0–L1–Y, la relación que se establece entre tratamiento y desenlace pasa por las variables confusoras L1. Para estimar el efecto, según los modelos clásicos, se podría utilizar una regresión sin considerar los confusores L1 puesto que están en la misma cadena causal entre el efecto (A0) y el desenlace (Y) (fig. 4).
Diagrama representativo de las variables confusoras tiempodependientes en los estudios observacionales. Podría suceder que se estableciera una relación entre la variable de exposición y el desenlace simplemente influido por la existencia de las variables confusoras tiempodependientes (camino alternativo en rojo) y no verdaderamente por la existencia de una relación causal entre la exposición y el desenlace.
Si se estima el efecto sin ajustar por L1, se estaría cometiendo un sesgo dado que no se estaría considerando el camino causal que hay entre A1 e Y que pasa por L1. Los métodos de regresión pueden presentar problemas de sesgo aunque no haya confusión residual; esto es debido posiblemente a la confusión creada por las variables tiempodependientes en la asignación del tratamiento previo.
Existen distintas alternativas para poder estimar el efecto de un tratamiento en presencia de confusores tiempodependientes: modelos estructurales marginales y modelos estructurales anidados20.
Los modelos marginales estructurales19 se consideran como alternativa a los modelos de regresión cuando existe una variable confusora tiempodependiente que se encuentra asociada con el desenlace de interés y que también se relaciona con el tratamiento que se está evaluando. La palabra estructural indica un efecto causal, no solo asociación estadística.
En lugar de la distribución conjunta se usan las distribuciones marginales, condicionadas a las variables basales, por lo que se denominan modelos marginales.
Estimación del efecto mediante un modelo marginal estructuralPara la creación de los modelos marginales estructurales, el primer paso es la estimación del IP mediante modelos de regresión logística o probit, en el cual la variable dependiente es el tratamiento y las independientes son aquellas variables asociadas con el inicio del tratamiento y/o con el evento de interés.
Cada paciente contribuye con tantas observaciones como unidades de tiempo se hayan seguido (meses, semanas…). Se deberá añadir como covariable la variable tiempo de seguimiento.
El peso de cada paciente y tiempo es estimado según las probabilidades predichas por este modelo, mediante el inverso de la probabilidad de tratamiento que realmente recibió. En este contexto, se asume que no hay eventos competitivos puesto que se considera que cada paciente es seguido hasta que ocurre el evento de interés o se pierde su seguimiento.
Del mismo modo que anteriormente, se estima un peso, para cada paciente, de ser censurado.
Mediante su producto, se combinan los pesos obtenidos del tratamiento y de la probabilidad de censura; de este modo, con esta ponderación, se puede simular una muestra en la que el tratamiento y la censura son independientes de los confusores medidos. En caso de que haya probabilidades muy pequeñas, los pesos extremos se sustituyen por percentiles cercanos21 (1 y 99 o 2,5 y 97,5) evitando así la presencia de valores de pesos muy grandes.
En el caso de que el evento de interés sea una variable binaria, la OR de la regresión logística entre el evento y el tratamiento, ponderada por el peso combinado, aproxima bien al riesgo relativo instantáneo del modelo de Cox, porque el riesgo de eventos es bajo en todos los meses.
AsuncionesPara poder utilizar los métodos estadísticos anteriormente descritos se deben verificar ciertas asunciones, como son:
- •
El orden temporal: es decir, que la exposición al tratamiento ocurra antes que el evento.
- •
Consistencia: el resultado potencial de un individuo, condicionado al historial del tratamiento observado, coincide con el verdadero resultado observado.
- •
Positividad: los individuos de la población deben presentar una probabilidad mayor de cero de recibir el tratamiento en cada categoría del tratamiento y en cada uno de los niveles de las variables confusoras. De este modo, el efecto causal promedio del tratamiento se puede estimar dentro de cada subgrupo de la población establecido por las variables confusoras.
- •
Correcta especificación del modelo: es decir, que se haya estimado el modelo de forma adecuada. La asunción de linealidad se debería evaluar.
- •
Ausencia de confusión residual: se puede comprobar mediante un análisis de sensibilidad puesto que no se puede asumir utilizando solo los datos de los pacientes.
La ventaja fundamental del IP es que resume en un solo número las características basales de los individuos en los que se realiza la investigación. Este índice resume con un número la probabilidad de ser expuesto.
Por ejemplo, si el objetivo del estudio es evaluar el efecto de la ventilación no invasiva en niños que ingresan en UCI en un estudio observacional de más de 30.000 pacientes de los cuales casi un tercio recibe como primera opción ventilación no invasiva, este tipo de pregunta de investigación se podría haber planteado, con dificultades, mediante un ensayo clínico22.
También se ha utilizado este tipo de análisis para estimar el efecto ajustado del cáncer en la mortalidad en UCI23, ya que esta investigación solo se puede contestar en investigación clínica mediante estudios observacionales.
También se podrían utilizar estas técnicas analíticas para estimar el efecto de una complicación como es la debilidad adquirida en la UCI (DACI) en el fracaso del weaning o en la mortalidad del paciente durante su estancia en UCI24,25.
Vamos a desarrollar este último ejemplo, paso a paso. Se trata de un estudio prospectivo, internacional y multicéntrico realizado con 4.157 pacientes con ventilación mecánica durante más de 12h. La aparición de DACI durante la estancia se asoció con más fracaso del weaning y con más mortalidad en UCI. El IP se estimó con las siguientes variables: edad, SAPS II al ingreso en UCI, motivo principal de inicio de la ventilación mecánica (EPOC, insuficiencia cardíaca, sepsis, SDRA y neumonía).
Para evaluar el efecto de la sedación y analgesia en pacientes con ventilación no invasiva en la necesidad de intubación endotraqueal y ante la presencia de confusores tiempodependientes como son la escala de sedación de RASS (Richmond Agitation-Sedation Scale), la PCO2 o el RASS es necesario plantear un modelo marginal estructural. Para ilustrar la utilización de estos métodos comparando las distintas opciones del IP, y mostrando los resultados mediante métodos clásicos como la regresión logística, se usará un conjunto de datos de un estudio multicéntrico de UCI con ventilación mecánica.
Primera parteTeniendo en cuenta como tratamiento la interrupción de la sedación y como evento el fallecimiento del paciente, se ha aplicado el IP para evaluar la causalidad. Aplicando diferentes modalidades del IP (matching, estratificación, IPTW y como covariable del modelo), para este escenario clínico, se han obtenido estimaciones en términos de OR e IC (95%) similares. Estas OR se han comparado con las que se obtienen estimando el efecto sin el IP (tabla 1).
Relación entre riesgo de mortalidad a día 28 (status día 28) y la interrupción de la sedación según diferentes estrategias de análisis de propensión
| Aplicaciones del Propensity score | Sin Propensity score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Emparejamiento | IPTW | Estratificación MH | Covariable | RL Univariante | RL Multivariante | |||||||
| OR | IC (95%) | OR | IC (95%) | OR | IC (95%) | OR | IC (95%) | OR | IC (95%) | OR | IC (95%) | |
| Status día 28 | 0,64 | (0,49; 0,83) | 0,67 | (0,52; 0,85) | 0,68 | (0,53; 0,86) | 0,67 | (0,52; 0,85) | 0,64 | (0,52; 0,80) | 0,63 | (0,49; 0,81) |
IC: intervalo de confianza; IPTW: inverse probability of treatment weighting; MH: Mantel-Haenszel; OR: odds ratio; RL: regresión logística.
Estos resultados tan similares se deben a que, en relación con las características basales, pacientes tratados y no tratados no difieren y por lo tanto el IP estimado es muy similar en ambos conjuntos de sujetos.
Segunda parteSi se considerase un conjunto de pacientes cuyas características basales presentaran más diferencias, las estimaciones obtenidas del efecto del tratamiento no concordarían en los diferentes métodos. Por ejemplo, si se considerase solo aquellos pacientes con enfermedades respiratorias y se quisiera estudiar el efecto de los bloqueantes neuromusculares sobre el delirio del paciente, se obtendrían estimaciones diferentes en los diferentes métodos (tabla 2).
Relación entre riesgo de mortalidad a dia 28 (status día 28) y la interrupción de la sedación según diferentes estrategias de análisis de propensión
| Aplicaciones del Propensity score | Sin Propensity score | ||||
|---|---|---|---|---|---|
| OR | IC (95%) | OR | IC (95%) | ||
| Emparejamiento | 1,72 | (0,55; 5,97) | Univariante | 2,79 | (1,26; 6,17) |
| IPTW | 2,08 | (0,83; 5,24) | Multivariante | 3,18 | (1,42; 7,13) |
| Estratificación | 1,81 | (1,14; 7,14) | |||
| Covariable | 2,06 | (0,84; 5,11) | |||
IC, intervalo de confianza; IPTW: inverse probability of treatment weighting: OR: odds ratio.
Los pesos obtenidos mediante el IPTW abarcan los siguientes valores: [1,037; 12,75].
Cuando pacientes tratados y no tratados difieren y el número de eventos y de exposiciones es reducido, se observan diferencias significativas entre los métodos estadísticos.
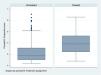
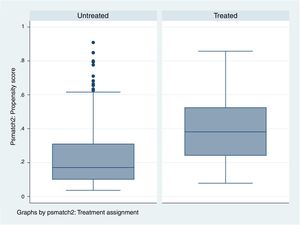
Para ver cómo se distribuyen los pacientes tratados y los no tratados mediante el IP estimado se estudia la zona de soporte común: es el rango de valores comunes que el IP presenta en ambos grupos.
Por lo tanto, cuanto más parecidos sean los grupos de tratados y no tratados, la zona de soporte común abarcará mayor cantidad de pacientes de ambos grupos.
Si tratados y no tratados son muy similares, la zona de soporte común abarcará todos los individuos porque el máximo y el mínimo de ambos IP serán parecidos. Si ambos grupos son muy distintos, lo más probable es que el número de pacientes que entren en la zona de soporte común sea más reducido (fig. 5) (tabla 3).
Comparación de las diferencias estandarizadas de las variables basales en pacientes tratados y no tratados, antes y después del emparejamiento para comprobar que el índice de propensión (IP) está especificado correctamente. Si estas diferencias son mayores en un 10% significará que el IP no está calculado de modo adecuado
| Antes del emparejamiento | Después del emparejamiento | |||||
|---|---|---|---|---|---|---|
| NMB=Sí (n=148) | NMB=No (n=390) | Diferencias estandarizadas (%) | NMB=Sí (n=141) | NMB=No (n=381) | Diferencias estandarizadas (%) | |
| Variables basales | ||||||
| Edad (años), media (DE) | 59,53 (13,53) | 65,33 (13,58) | 42,79 | 60,53 (14,53) | 58,96 (13,64) | 11,17 |
| SAPS_II puntos), media (DE) | 43,74 (15,49) | 46,83 (16,76) | 19,15 | 44,99 (15,67) | 43,41 (14,78) | 10,37 |
| Sexo (V) | 56,8 | 48,5 | 16,63 | 55 | 58,3 | 6,73 |
| Soporte ventilatorio invasivo (Sí) | 21,6 | 21,3 | 0,59 | 23,3 | 21,7 | 3,98 |
| Presencia de fracaso cardiovascular (Sí) | 68,9 | 40,8 | 58,37 | 67,5 | 68,3 | 1,78 |
| Presencia de fracaso renal (Sí) | 42,6 | 21,28 | 40,87 | 36,7 | 40 | 6,85 |
| Presencia de fracaso hematológico (Sí | 24,3 | 8,97 | 25,75 | 19,2 | 16,7 | 6,52 |
| Sepsis durante la ventilación mecánica | 43,24 | 24,1 | 37 | 40,88 | 45,83 | 10,10 |
| Duración de soporte ventilatorio (días) | 15,90±13,14 | 8,21±14,82 | 54,91 | 14,35±11,60 | 11,97±19,04 | 15,09 |
Para ver si el orden de los sujetos en el método del emparejamiento influye, se han realizado (simulado) 100 modelos y se han obtenido las correspondientes estimaciones de las OR. Se ha observado que cuando el número de variables por las que se ajusta el IP es elevado, el orden de emparejamiento no influye y se obtienen estimaciones similares. Cuando el número de variables por las que se ajusta el orden de emparejamiento sí que influye, se obtienen estimaciones diferentes.
Ventajas e inconvenientes de estas técnicasSe ha comprobado que, dependiendo del número de eventos y de exposiciones que haya, el IP y la regresión logística podrían considerarse equivalentes, obteniendo valores en las estimaciones similares cuando no se observan diferencias entre pacientes tratados y no tratados y el número de eventos es elevado.
Cuando el número de eventos es reducido, el IP permite ser ajustado por más variables que la regresión logística, y además, permite cuantificar el efecto del tratamiento.
Mediante el método del emparejamiento del IP, se obtiene una estructura semejante a la de un ensayo clínico (las parejas presentan características similares), con la desventaja de que aquellos pacientes que no encuentren pareja serán descartados del estudio.
Los ensayos clínicos aleatorizados presentan la ventaja de que, debido a la asignación aleatoria del paciente, se puede evaluar la relación causal de modo directo. Cuando estos estudios no son viables, los estudios observacionales pueden considerarse como alternativa. Para poder evaluar la causalidad en estudios observacionales, se deberá resolver primero el problema de la confusión que conllevan dichos estudios.
ConclusionesLos ensayos clínicos representan el mejor diseño metodológico para analizar la causalidad en investigación clínica. Sin embargo, existen hipótesis que no pueden ser testadas clínicamente por limitaciones éticas, metodológicas, económicas. Para resolver esta limitación los estudios observacionales pueden abordar este problema y simular el escenario hipotético de un ensayo clínico para poder dar respuesta, mediante la aplicación del IP y los modelos marginales estructurales. El interés creciente por esta nueva metodología hace necesaria su difusión por todos los intensivistas para mejorar el conocimiento de esta metodología y su potencial aplicación en la investigación clínica de los Cuidados Intensivos.
Por ejemplo, Delaney et al.21 muestran el uso de los métodos estadísticos detallados en este artículo para evaluar el efecto de los corticoides sobre la mortalidad en pacientes que presentan gripe A (H1N1pdm09). Las OR asociadas a dichos modelos varían desde 1,85 (IC 95%: 1,12-3,04) en los modelos clásicos de regresión logística multivariable; 1,71 (IC 95%: 1,05-2,78) en el modelo de regresión logística ajustando por el IP; 1,52 (IC 95%: 0,90-2,58) después del emparejamiento del IP, y 0,96 (IC 95%: 0,28-3,28) en el modelo marginal estructural ajustando por las variables tiempodependientes. Ajustando mediante las variables tiempodependientes en los modelos marginales estructurales, han observado que no existe asociación entre el uso de corticoides y la mortalidad de los pacientes.
Conflicto de interesesLos autores del manuscrito declaran no tener ningún conflicto de intereses ni económico, ni comercial ni intelectual en la redacción de este artículo.